1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
| import sophon
import sophon.neuralNetwork.layers as layers
from sophon.neuralNetwork.nn import sequence
import matplotlib.pyplot as plt
def load_coffee_data(trainSize:int, testSize:int):
"""
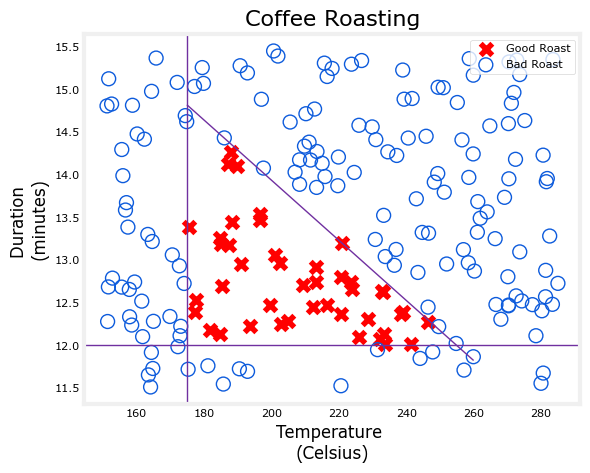
创建靠咖啡的时间和温度的数据
烘烤时间: 在 12-15 分钟之间最佳
温度范围: 在 175-260 C 之间最佳
Parameters
----------
trainSize : int
训练集大小
testSize : int
测试集大小
Returns
-------
TYPE
训练集和测试集
"""
rng = np.random.default_rng(2)
X = rng.random((trainSize + testSize) * 2).reshape(-1,2)
X[:,0] = X[:,0] * (285-150) + 150
X[:,1] = X[:,1] * 4 + 11.5
Y = np.zeros(len(X))
i=0
for t,d in X:
y = -3/(260-175)*t + 21
if (t > 175 and t < 260 and d > 12 and d < 15 and d<=y ):
Y[i] = 1
else:
Y[i] = 0
i += 1
Y = Y.reshape(-1, 1)
return X[:trainSize, :], Y[:trainSize, :], X[trainSize:,:], Y[trainSize:, :]
print("\n靠咖啡豆测试")
train_x, train_y, test_x, test_y = load_coffee_data(400, 50)
mu = np.mean(train_x, axis=0, keepdims=True)
sigma = np.std(train_x, axis=0, keepdims=True)
train_x_norm = somath.normalize(train_x, mu, sigma)
test_x_norm = somath.normalize(test_x, mu, sigma)
nnet = sequence(train_x_norm.shape[1:],
[layers.dense(3, "sigmoid"),
layers.dense(1, "sigmoid")],
1234)
nnet.showOutputShape()
nnet.options(lr = 0.01, optimizer=opt.adam())
history = nnet.fit(train_x_norm, train_y, epochs=5000)
W1 = nnet.layerList[0].weight
b1 = nnet.layerList[0].bias
W2 = nnet.layerList[1].weight
b2 = nnet.layerList[1].bias
print(f"成本记录:\n{history}")
print(f"第一层权重:\n{W1}")
print(f"第一层偏移量:\n{b1}")
print(f"第二层权重:\n{W2}")
print(f"第二层偏移量:\n{b2}")
print("训练数据原始图像:")
plt.scatter(train_x[:, 0], train_x[:, 1], c=train_y[:, 0])
plt.show()
prob_y = nnet.prediction(train_x_norm)
pre_y = np.where(prob_y >= 0.5, 1, 0)
print("训练数据预测图像:")
plt.scatter(train_x[:, 0], train_x[:, 1], c=pre_y[:, 0])
plt.show()
acc = np.sum(pre_y == train_y) / pre_y.shape[0]
print(f"训练数据准确率:{acc}")
print("测试数据原始图像:")
plt.scatter(test_x[:, 0], test_x[:, 1], c=test_y[:, 0])
plt.show()
prob_y = nnet.prediction(test_x_norm)
pre_y = np.where(prob_y >= 0.5, 1, 0)
print("测试数据预测图像:")
plt.scatter(test_x[:, 0], test_x[:, 1], c=pre_y[:, 0])
plt.show()
acc = np.sum(pre_y == test_y) / pre_y.shape[0]
print(f"测试数据准确率:{acc}")
|