是谁在国庆节还在打比赛？原来是我啊！本次周赛参加比赛的人都少了很多，而且题目也简单不少，顺利 AK。

战局详情

排名	用户名	得分	完成时间	题目1（3）	题目2（4）	题目3（5）	题目4（6）
271 / 2909	Juruoer	18	1:21:22	0:04:07	0:14:14 1	0:33:48 1	1:11:22

题目及解答

有序三元组中的最大值 I

100088. 有序三元组中的最大值 I

给你一个下标从 0 开始的整数数组 nums 。

请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中，找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数，则返回 0 。

下标三元组 (i, j, k) 的值等于 (nums[i] - nums[j]) * nums[k] 。

提示：

3 <= nums.length <= 100
1 <= nums[i] <= 1e6

示例一：

输入：nums = [12,6,1,2,7]
输出：77
解释：下标三元组 (0, 2, 4) 的值是 (nums[0] - nums[2]) * nums[4] = 77 。
可以证明不存在值大于 77 的有序下标三元组。

示例二：

1
2
3

输入：nums = [1,2,3]
输出：0
解释：唯一的下标三元组 (0, 1, 2) 的值是一个负数，(nums[0] - nums[1]) * nums[2] = -3 。因此，答案是 0 。

解决方案：

由于数据量较小，直接暴力即可。

代码：

class Solution {
public:
    long long maximumTripletValue(vector<int>& nums) {
        long long rst = 0;
        for(int i = 0; i < nums.size(); ++i)
        {
            for(int j = i + 1; j < nums.size(); ++j)
            {
                for(int k = j + 1; k < nums.size(); ++k)
                {
                    rst = max(rst, 1LL * (nums[i] - nums[j]) * nums[k]);
                }
            }
        }
        return rst;
    }
};

时间复杂度： $O(n^3)$ ；空间复杂度： $O(1)$ 。n 为 nums 的长度。

有序三元组中的最大值 II

100086. 有序三元组中的最大值 II

给你一个下标从 0 开始的整数数组 nums 。

请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中，找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数，则返回 0 。

下标三元组 (i, j, k) 的值等于 (nums[i] - nums[j]) * nums[k] 。

提示：

3 <= nums.length <= 1e5
1 <= nums[i] <= 1e6

示例一：

输入：nums = [12,6,1,2,7]
输出：77
解释：下标三元组 (0, 2, 4) 的值是 (nums[0] - nums[2]) * nums[4] = 77 。
可以证明不存在值大于 77 的有序下标三元组。

示例二：

输入：nums = [1,10,3,4,19]
输出：133
解释：下标三元组 (1, 2, 4) 的值是 (nums[1] - nums[2]) * nums[4] = 133 。
可以证明不存在值大于 133 的有序下标三元组。

示例三：

1
2
3

输入：nums = [1,2,3]
输出：0
解释：唯一的下标三元组 (0, 1, 2) 的值是一个负数，(nums[0] - nums[1]) * nums[2] = -3 。因此，答案是 0 。

解决方案：

模拟：

本题与上一题一模一样，但是数据量比较大，暴力一定超时。

观察 (nums[i] - nums[j]) * nums[k]，需要获得此数值的最大值即需要获得 (nums[i] - nums[j]) 的最大值和 nums[k] 的最大值，其中 j < k。

我们可以先用数组 max_nums 来记录 nums 的最大值，其中 max_nums[i] 表示 nums[0] ~ nums[i] 的最大值。

然后用数组 max_subs 来记录两数只差的最大值，其中 max_subs[idx] 表示 nums[i] - nums[j] 的最大值，其中 i < j <= idx 。

最后计算出结果。

代码：

class Solution {
public:
    long long maximumTripletValue(vector<int>& nums) {
        int n = nums.size();
        int max_nums[n];
        max_nums[0] = nums[0];
        for(int i = 1; i < n; ++i)
            max_nums[i] = max(max_nums[i - 1], nums[i]);
        int max_subs[n];
        max_subs[0] = 0;
        for(int j = 1; j < n; ++j)
            max_subs[j] = max(max_subs[j - 1], max_nums[j - 1] - nums[j]);
        long long rst = 0;
        for(int k = 2; k < n; ++k)
            rst = max(rst, 1LL * nums[k] * max_subs[k - 1]);
        return rst;
    }
};

时间复杂度： $O(n)$ ，空间复杂度： $O(n)$ 。n 为数组 nums 的长度。

无限数组的最短子数组

100076. 无限数组的最短子数组

给你一个下标从 0 开始的数组 nums 和一个整数 target 。

下标从 0 开始的数组 infinite_nums 是通过无限地将 nums 的元素追加到自己之后生成的。

请你从 infinite_nums 中找出满足 元素和 等于 target 的最短子数组，并返回该子数组的长度。如果不存在满足条件的子数组，返回 -1 。

提示：

1 <= nums.length <= 1e5
1 <= nums[i] <= 1e5
1 <= target <= 1e9

示例一：

输入：nums = [1,2,3], target = 5
输出：2
解释：在这个例子中 infinite_nums = [1,2,3,1,2,3,1,2,...] 。
区间 [1,2] 内的子数组的元素和等于 target = 5 ，且长度 length = 2 。
可以证明，当元素和等于目标值 target = 5 时，2 是子数组的最短长度。

示例二：

输入：nums = [1,1,1,2,3], target = 4
输出：2
解释：在这个例子中 infinite_nums = [1,1,1,2,3,1,1,1,2,3,1,1,...].
区间 [4,5] 内的子数组的元素和等于 target = 4 ，且长度 length = 2 。
可以证明，当元素和等于目标值 target = 4 时，2 是子数组的最短长度。

示例三：

输入：nums = [2,4,6,8], target = 3
输出：-1
解释：在这个例子中 infinite_nums = [2,4,6,8,2,4,6,8,...] 。
可以证明，不存在元素和等于目标值 target = 3 的子数组。

解决方案：

设 nums 的元素和为 sum。

一、 target 小于 sum

只需要将 nums 看作一个 环形数组，并找出此环形数组的一个最短连续子数组，使之元素和为 target 即可，我们可以使用一个临时数组 _nums 来模拟此环形数组，其中 _nums 为两个 nums 连接而成。

利用前缀和 pre_sum 来记录 _nums 的前缀和，若两个前缀和之差为 target ，那么即存在元素和为 target 的子数组，子数组长度即两前缀和所累加的元素的个数之差，需要找到最小的子数组的长度。

另外，如果使用双重循环来寻找两个差为 target 的前缀和会超时，我们需要一个哈希表来记录前缀和以及此前缀和所累加的元素的个数。

二、target 大于 sum

若存在子数组和为 target ，则此子数组包含 target / sum 个 nums。并且我们需要按照上述一中的方法找到元素和为 target % sum 的子数组的最短长度，假设为 x，则和为 target 的最短子数组长度为 targe / sum * n + x ，n 为 nums 的长度。

代码：

class Solution {
public:
    int minSizeSubarray(vector<int>& nums, int target) {
        int n = nums.size(), m = 2 * n;
        long long sum = accumulate(nums.begin(), nums.end(), 0LL);
        int t = target / sum; // 子数组若存在，则需要 t 个 nums
        target = target % sum; // 实际在 nums 中寻找元素和为 target % sum 的子数组
        if(target == 0)
            return t * n;
        vector<int> _nums(m); // 模拟循环数组
        for(int i = 0; i < n; ++i)
            _nums[i] = nums[i];
        for(int i = n; i < m; ++i)
            _nums[i] = nums[i - n];
        unordered_map<long long, int> pre_sum; // 用哈希表来记录前缀和及其所累加的元素的个数
        pre_sum[0] = 0;
        sum = 0;
        int x = n;
        for(int i = 0; i < m; ++i)
        {
            sum += _nums[i];
            if(pre_sum.count(sum - target))
                x = min(x, i + 1 - pre_sum[sum - target]);
            pre_sum[sum] = i + 1;
        }
        return x == n ? -1 : t * n + x;
    }
};

时间复杂度： $O(n)$ ；空间复杂度： $O(n)$ 。n 为 nums 的长度。

有向图访问计数

100075. 有向图访问计数

现有一个有向图，其中包含 n 个节点，节点编号从 0 到 n - 1 。此外，该图还包含了 n 条有向边。

给你一个下标从 0 开始的数组 edges ，其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的边。

想象在图上发生以下过程：

你从节点 x 开始，通过边访问其他节点，直到你在 此过程 中再次访问到之前已经访问过的节点。

返回数组 answer 作为答案，其中 answer[i] 表示如果从节点 i 开始执行该过程，你可以访问到的不同节点数。

提示：

n == edges.length
2 <= n <= 1e5
0 <= edges[i] <= n - 1
edges[i] != i

示例一：

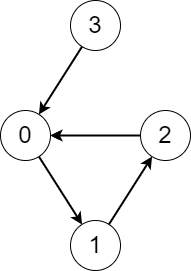
输入：edges = [1,2,0,0]
输出：[3,3,3,4]
解释：从每个节点开始执行该过程，记录如下：
- 从节点 0 开始，访问节点 0 -> 1 -> 2 -> 0 。访问的不同节点数是 3 。
- 从节点 1 开始，访问节点 1 -> 2 -> 0 -> 1 。访问的不同节点数是 3 。
- 从节点 2 开始，访问节点 2 -> 0 -> 1 -> 2 。访问的不同节点数是 3 。
- 从节点 3 开始，访问节点 3 -> 0 -> 1 -> 2 -> 0 。访问的不同节点数是 4 。

示例二：
示例二图

1
2
3

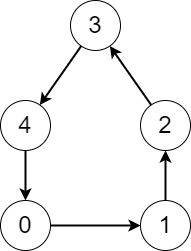
输入：edges = [1,2,3,4,0]
输出：[5,5,5,5,5]
解释：无论从哪个节点开始，在这个过程中，都可以访问到图中的每一个节点。

解决方案：

深度优先搜索：

因为 n 个节点只有 n 条边，并且每个节点有且只有一个出边，所有整个图可以看作是若干个类似于示例一所示的最小连通子图，该子图由一个 x 个节点组成的环和由 y 个节点组成的长链，此长链最后指向环，其中 x > 0 , y >= 0 。

对每一个未计算出结果的节点，我们可以使用一次深度优先搜索来计算此节点的结果，以及此节点的后继结点及子孙节点的结果。为方便，我们以示例一为案例来表述计算过程，其他所有的情况可以看作是示例一的拓展（有更多或更少的节点组成的长链或者有更多或更少节点组成的环）。

假设我们先计算节点 3 的结果（虽然后续的代码中我们会从 0 开始计算结果，但这并不重要），那么他会先计算它的后继 0 的结果，并将自身（节点 3）置为已访问，在递归计算的过程中，一定为访问到某个节点，此节点之前已经访问过（这是由 n 个节点 n 条边，且每个节点有且只有一个出边所决定的必然结果），在此案例中为节点 0 那么从第一次访问到 0 到再次访 0 过程中所访问的所有节点组成一个环，此环中所有节点的结果即环的长度，最终在计算节点 0 那一层的递归会返回节点 0 的结果，节点 3 在受到此结果后，将其加 1 即节点 3 的结果。

倘若有一个节点 4 指向节点 3，并且节点 3 的结果已经计算出来了，那么在其递归计算节点 3 的时候就不用继续递归了，直接返回节点 3 的结果即可。

但是按照若如上方法，我们只能判断 0 节点是环内的节点，对于其他节点无法判断是环内还是环外，我们发现，只有对于环内的节点而言，其后继节点所返回的值是有效的，代表后继节点的结果，对于环内的节点而言，其结果都是环的长度，我们可以从第二个访问到相同节点开始，其递归返回的节点即此节点的相反数，用于代表此环的入口。那么，当某次递归计算时，发现其向下递归的返回值大于 0，则表示此次计算的结果不在环内，返回值表示其后继节点的结果，否则表示当前节点在环内，返回值为环的起点，此节点的结果与环起点的结果相同，均为环的长度。对案例一而言，第二次访问 0 已经访问 1 和 2 时，返回的结果均为 0，表示环的起点为 0，而第一次访问 0 时，其返回的结果为 3 ，表示 0 的结果为 3，然后节点 3 的结果在此基础上加一，结果为 4。

代码：

class Solution {
private:
    vector<int> rst; // 结果集
    vector<int> used; // 访问标记，当值为 0 时表示未访问，否则表示访问到此节点已经访问的节点个数，用于计算环的长度
    int func(vector<int> &edges, int node, int len)
    {
        if(rst[node]) // 若结果已经计算过，那么直接返回，这种情况只存在与其前驱节点在直连上
            return rst[node];
        if(used[node]) // 已经访问过，说明出现了环，并且 node 为环起点
        {
            rst[node] = len - used[node]; // 计算环长度
            return -node; // 返回环起点的相反数，告知其前驱节点，此时在环内
        }
        used[node] = len; // 访问标记表示访问到此节点已经访问的节点个数，用于计算环的长度
        int x = func(edges, edges[node], len + 1); // 后继节点的返回值
        if(x > 0) // 表示当前节点在长链上，且返回值即后继结点的结果
        {
            rst[node] = x + 1;
            return rst[node];
        }
        else // 表示当前节点在环上，返回值为环起点的相反数
        {
            if(node == -x) // 表示当前节点即环起点，并且向上返回结果
                return rst[node];
            rst[node] = rst[-x];
            return x;
        }
    }
public:
    vector<int> countVisitedNodes(vector<int>& edges) {
        int n = edges.size();
        rst = vector<int>(n, 0);
        used = vector<int>(n, 0);
        for(int i = 0; i < n; ++i)
            if(rst[i] == 0)
                func(edges, i, 1);
        return rst;
    }
};

时间复杂度： $O(n)$ ；空间复杂度： $O(n)$ 。n 为节点个数。

记录 LeetCode 第 365 场周赛

战局详情

题目及解答