前两天刷 LeetCode 每日一题的时候，遇到一道不错的并查集题目。

原题

1632. 矩阵转换后的秩

给你一个 m x n 的矩阵 matrix ，请你返回一个新的矩阵 answer ，其中 answer[row][col] 是 matrix[row][col] 的秩。

每个元素的 秩 是一个整数，表示这个元素相对于其他元素的大小关系，它按照如下规则计算：

秩是从 1 开始的一个整数。
如果两个元素 p 和 q 在 同一行 或者 同一列 ，那么：

  • 如果 p < q ，那么 rank(p) < rank(q)
  • 如果 p == q ，那么 rank(p) == rank(q)
  • 如果 p > q ，那么 rank(p) > rank(q)

秩 需要越 小 越好。
题目保证按照上面规则 answer 数组是唯一的。

示例 1：

示例 1

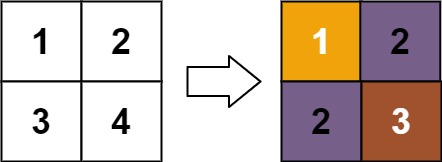
输入：matrix = [[1,2],[3,4]]

输出：[[1,2],[2,3]]

解释：

matrix[0][0] 的秩为 1 ，因为它是所在行和列的最小整数。

matrix[0][1] 的秩为 2 ，因为 matrix[0][1] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。

matrix[1][0] 的秩为 2 ，因为 matrix[1][0] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。

matrix[1][1] 的秩为 3 ，因为 matrix[1][1] > matrix[0][1]， matrix[1][1] > matrix[1][0] 且 matrix[0][1] 和 matrix[1][0] 的秩都为 2 。

示例2：

示例 2

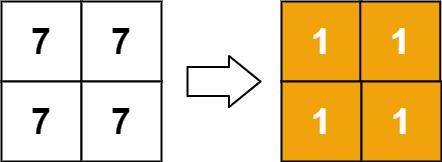
输入：matrix = [[7,7],[7,7]]

输出：[[1,1],[1,1]]

示例 3：

示例 3

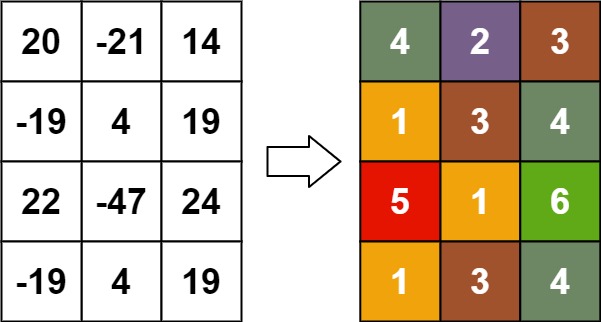
输入：matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]

输出：[[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

示例 4：

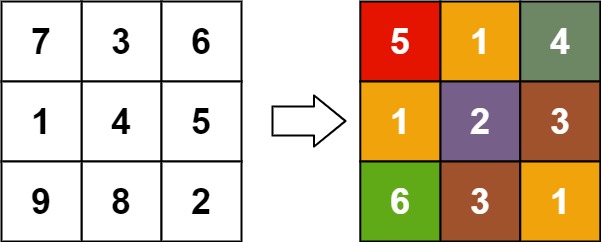
输入：matrix = [[7,3,6],[1,4,5],[9,8,2]]

输出：[[5,1,4],[1,2,3],[6,3,1]]

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • -1e9 <= matrix[row][col] <= 1e9

注意事项

此题有一个翻译错误，英文版的题目中使用的 rank 不应该翻译成 秩，因为矩阵的秩在线性代数中是有定义的，在下面的题解中我将使用 rank 来代替 秩。

要解决该题，需要的前置知识：并查集、拓扑排序。

朴素的想法

首先我们思考一种简单的情况：矩阵中没有相同的元素。

如果一个元素其所在的行、列中比值它小的元素的 rank 已经确定了，那么该元素的 rank 应该是对少呢？

很显然，该元素的 rank 值比它所在的行中的所有比它小的元素的 rank 大，也比它所在列中的所有比它小的元素的的 rank 大，并且要求每个元素的 rank 值取最小。

那么我们只需要按元素值大小从小打到遍历每一个元素，然后查看其所在行、列中比它小的元素中 rank 值最大的元素的 rank 值是多少（假设为 r），那么该元素的 rank 值就是 r + 1。由于是从小到大遍历，所以在遍历各元素时，比它小的元素的 rank 值已经求出。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution
{
public:
    typedef pair<int, int> pii;
    vector<vector<int>> matrixRankTransform(vector<vector<int>> &matrix)
    {
        int m = matrix.size(), n = matrix[0].size(), t = m * n;
        pii nums[t]; // 记录 matrix 中每个数字的下标，因为我们需要根据元素值找到其在矩阵中的行和列
        vector<vector<int>> rst(m, vector<int>(n));
        for (int i = 0, k = 0; i < m; ++i)
        {
            for (int j = 0; j < n; ++j, ++k)
            {
                nums[k].first = i;
                nums[k].second = j;
            }
        }
        sort(nums, nums + t, [&](const pii &a, const pii &b) // 根据元素大小排序
             { return matrix[a.first][a.second] < matrix[b.first][b.second]; });
        int rowHave[m]; // rowHave[i] 记录第 i 行已有的最大 rank
        int colHave[n]; // colHave[j] 记录第 j 列已有的最大 rank
        memset(rowHave, 0, sizeof(rowHave));
        memset(colHave, 0, sizeof(colHave));
        for (pii &x : nums) // 按从小到大遍历所有元素
        {
            int num = matrix[x.first][x.second]; // num 是位于 x.first 行，x.second 列的元素
            int rr = rowHave[x.first];    // num 所在行已有的最大 rank
            int cr = colHave[x.second];   // num 所在列已有的最大 rank
            rst[x.first][x.second] = rowHave[x.first] = colHave[x.second] = max(rr, cr) + 1; // 取得 num 的 rank 值并更新其所在行、列已有的最大 rank
        }
        return rst;
    }
};

现在的问题是，存在相同的元素，如果仍然使用上述代码会怎样？

运行示例 2，会发现结果为：[[1,2],[2,3]]。

一种直观的修改方案是：

不仅记录各行与各列已有的最大 rank（假设为 r），而且记录该 rank 的元素值，如果当前元素与最大 rank 的元素值相同，那么该元素的 rank 也为 r，否则为 r + 1。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution
{
public:
    typedef pair<int, int> pii;
    vector<vector<int>> matrixRankTransform(vector<vector<int>> &matrix)
    {
        int m = matrix.size(), n = matrix[0].size(), t = m * n;
        pii nums[m * n]; // 记录 matrix 中每个数字的下标，因为我们需要根据元素值找到其在矩阵中的行和列
        vector<vector<int>> rst(m, vector<int>(n));
        for (int i = 0, k = 0; i < m; ++i)
        {
            for (int j = 0; j < n; ++j, ++k)
            {
                nums[k].first = i;
                nums[k].second = j;
            }
        }
        sort(nums, nums + t, [&](const pii &a, const pii &b) // 根据元素大小排序
             { return matrix[a.first][a.second] < matrix[b.first][b.second]; });
        pii rowHave[m]; // rowHave[i] 记录第 i 行已有的最大 rank 及其元素值
        pii colHave[n]; // colHave[j] 记录第 j 列已有的最大 rank 及其元素值
        for (int i = 0; i < m; ++i)
            rowHave[i].first = 0;
        for (int j = 0; j < n; ++j)
            rowHave[j].first = 0;
        for (pii &x : nums) // 按从小到大遍历所有元素
        {
            int num = matrix[x.first][x.second];
            int rr = rowHave[x.first].first + ((rowHave[x.first].first == 0) || (rowHave[x.first].second != num)); // num 在行的限制下的最小 rank（与上一个代码的含义稍微不同）
            int cr = colHave[x.second].first + ((colHave[x.second].first == 0) || (colHave[x.second].second != num)); // num 在列的限制下的最小 rank（与上一个代码的含义稍微不同）
            rst[x.first][x.second] = rowHave[x.first].first = colHave[x.second].first = max(rr, cr); // 取得 num 的 rank 并更新行、列已有的最大 rank，取两限制下的最大值
            rowHave[x.first].second = colHave[x.second].second = num; // 更新行、列已有的最大 rank 的数的值
        }
        return rst;
    }
};

在运行示例 2，结果正确，但提交后发现 WA：

输入：[[-37,-50,-3,44],[-37,46,13,-32],[47,-42,-3,-40],[-17,-22,-39,24]]

输出：[[2,1,3,6],[2,6,5,4],[5,2,4,3],[4,3,1,5]]

预期：[[2,1,4,6],[2,6,5,4],[5,2,4,3],[4,3,1,5]]

发现第 0 行第 2 列的 rank 值应该是 4，但上述代码计算得出为 3。

原因在于，我们先计算了第 0 行第 2 列的 -3 的 rank 值为 3 后，再计算第 2 行第 2 列的 -3 的 rank 值，并发现其为 4，根据题干要求，同一行（列）相同元素的 rank 值应该相同，那么当我们计算完第 2 个 -3 的 rank 后应该把与其同行（列）的同为 -3 的且已经计算完 rank 值的元素的 rank 值也更新为 4。

这也就是这道题的难点。

最终的方案

经过以上分析，发现位于同一行、同一列的相同的元素的 rank 值相同，所以应该将其视为一个整体，并计算该整体的 rank 值，这与这个整体中每个元素所在行、列都有关。

假设有两个整体 s1 和 s2，元素值分别为 a 和 b，如果整体 s1 中存在某个元素 n1 与 s2 中的另一个元素 n2 同行或者同列，那么 a、b 一定不相等，否则由于 n1、n2 同行或同列，s1 和 s2 应该为同一个整体。若 a < b，则 s1 的 rank 小于 s2 的 rank，反之则反。

如果将每个整体视为一个结点，并且 rank 值小的结点有一条指向 rank 值大的结点的有向边（或有向路径），形成一个有向无循环图，就可以通过拓扑排序来得出每个整体的 rank 值。

那么如何构建这个有向无循环图呢？

在每一行（列）中，按元素值去重，再对去重后该行（列）的元素进行排序，排行后相邻的元素中，元素值小的元素所在的整体就有一条指向元素值大的元素所在的整体的有向边，对每一行（列）执行该过程，就形成了一个满足要求的有向无循环图（有点像织毛衣的感觉）。去重是因为同一行（列）中相同的元素属于一个整体。

现在的问题是，各整体如何表示？容易想到使用并查集来维护各个整体。

最后的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
typedef pair<int, int> pii;

class UnionFind // 并查集类
{
    vector<vector<pii>> roots; // 并查集中的各个元素的根节点，记录根节点的下标

public:
    UnionFind(int m, int n) // 构造函数，初始时个元素的根节点为其自身
    {
        roots = vector<vector<pii>>(m, vector<pii>(n));
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                roots[i][j] = make_pair(i, j);
    }

    pii find(int i, int j) // 查询在矩阵中下标为 (i, j) 的元素的根节点
    {
        pii r = roots[i][j];
        if(r.first != i || r.second != j)
            roots[i][j] = find(r.first, r.second);
        return roots[i][j];
    }

    void unio(int i1, int j1, int i2, int j2) // 将矩阵中下标为 (i1, j1) 和下标为 (i2, j2) 的两个元素所在的集合合并为一个集合
    {
        pii r1 = find(i1, j1), r2 = find(i2, j2);
        if(r1 != r2)
            roots[r2.first][r2.second] = r1;
    }
};

class Solution
{
public:
    vector<vector<int>> matrixRankTransform(vector<vector<int>> &matrix)
    {
        int m = matrix.size(), n = matrix[0].size();
        UnionFind uf(m, n); // 并查集

        // 构建并查集，使相同行或相同列且值相同的元素合并为一个集合，同一个集合中的所有元素的 rank 相同
        for (int i = 0; i < m; ++i)
        {
            unordered_map<int, vector<int>> num2indexList; // 记录第 i 行中相同元素的列下标
            for (int j = 0; j < n; ++j)                    // 将同一行中，相同的元素的列下标放入一个列表中
                num2indexList[matrix[i][j]].emplace_back(j);
            for (auto [_, indexList] : num2indexList)
            {
                int t = indexList[0];
                for (int k = 1; k < indexList.size(); ++k) // 将同一行中，相同元素放入合并为一个集合
                    uf.unio(i, t, i, indexList[k]);
            }
        }
        for (int j = 0; j < n; ++j)
        {
            unordered_map <int, vector<int>> num2indexList; // 记录第 j 列中相同元素的行下标
            for (int i = 0; i < m; ++i)                     // 将同一列中，相同元素的行下标放入一个列表中
                num2indexList[matrix[i][j]].emplace_back(i);
            for(auto [_, indexList] : num2indexList)
            {
                int t = indexList[0];
                for (int k = 1; k < indexList.size(); ++k) // 将同一列中，相同元素放入合并为一个集合
                    uf.unio(t, j, indexList[k], j);
            }
        }

        // 将每个集合看作一个结点，结点的值为该集合的根节点的下标的一维展开值，即下标 (i, j) 展开为 i * n + j
        // 若某个集合 s1 中存在一个元素小于与其同行或同列的另一个元素，且该元素在集合 s2 中，那么集合 s1 的 rank 小于集合 s2 的 rank
        // 那么集合 s1 的结点有一条指向集合 s2 的结点的有向边（或路径），可以通过拓扑排序来确定所有集合的 rank 的大小关系，第 i 大的集合，rank 为 i
        unordered_map<int, int> inDegrees; // 每个结点的入度
        unordered_map<int, vector<int>> outEdges; // 每个结点的出边
        for (int i = 0; i < m; ++i) // 初始化入度
        {
            for (int j = 0; j < n; ++j)
            {
                pii r = uf.find(i, j);
                inDegrees[r.first * n + r.second] = 0;
            }
        }

        // 构建图
        for (int i = 0; i < m; ++i)
        {
            unordered_map<int, int> num2index; // 记录同一行中相同元素中任意一个元素的列下标，用于去重
            for (int j = 0; j < n; ++j)
                num2index[matrix[i][j]] = j;
            vector<int> sortArr; // 记录同一行中所有的元素，相同元素只保存一个，并排序
            for(auto [key, _] : num2index)
                sortArr.emplace_back(key);
            sort(sortArr.begin(), sortArr.end());
            // 如果一个元素 num1 小于其所在行中的另一个元素 num2，那么 num1 所在的集合 s1 的 rank 小于 num2 所在集合 s2 的 rank，s1 有一条指向 s2 的有向边（或路径）
            for (int k = 1; k < sortArr.size(); ++k)
            {
                pii r1 = uf.find(i, num2index[sortArr[k - 1]]);
                pii r2 = uf.find(i, num2index[sortArr[k]]);
                int idx1 = r1.first * n + r1.second;
                int idx2 = r2.first * n + r2.second;
                // r1 指向 r2
                ++inDegrees[idx2];
                outEdges[idx1].emplace_back(idx2);
            }
        }
        for (int j = 0; j < n; ++j)
        {
            unordered_map<int, int> num2index; // 记录同一列中相同元素中任意一个元素的行下标，用于去重
            for (int i = 0; i < m; ++i)
                num2index[matrix[i][j]] = i;
            vector<int> sortArr; // 记录同一列中所有的元素，相同元素只保存一个，并排序
            for (auto [key, _] : num2index)
                sortArr.emplace_back(key);
            sort(sortArr.begin(), sortArr.end());
            // 如果一个元素 num1 小于其所在列中的另一个元素 num2，那么 num1 所在的集合 s1 的 rank 小于 num2 所在集合 s2 的 rank，s1 有一条指向 s2 的有向边（或路径）
            for (int k = 1; k < sortArr.size(); ++k)
            {
                pii r1 = uf.find(num2index[sortArr[k - 1]], j);
                pii r2 = uf.find(num2index[sortArr[k]], j);
                int idx1 = r1.first * n + r1.second;
                int idx2 = r2.first * n + r2.second;
                // r1 指向 r2
                ++inDegrees[idx2];
                outEdges[idx1].emplace_back(idx2);
            }
        }

        // 拓扑排序并计算集合（根）的 rank
        queue<int> q, temp;
        for (auto [key, dgeress] : inDegrees)
            if(dgeress == 0)
                q.emplace(key);

        int r = 1; // 当前的 rank
        while(q.size())
        {
            while(q.size())
            {
                int u = q.front();
                q.pop();
                matrix[u / n][u % n] = r;
                for(int v : outEdges[u])
                {
                    --inDegrees[v];
                    if(inDegrees[v] == 0)
                        temp.emplace(v);
                }
            }
            ++r;
            swap(q, temp);
        }

        // 元素的 rank 与其根的 rank 相同
        for (int i = 0; i < m; ++i)
        {
            for (int j = 0; j < n; ++j)
            {
                pii r = uf.find(i, j);
                matrix[i][j] = matrix[r.first][r.second];
            }
        }

        return matrix;
    }
};