本次周赛 依旧只写出前三题，第四题动态规划转移方程想了很久没整出来 (明明很简单！) 。

战局详情

排名用户名得分完成时间题目1（3）题目2（5）题目3（5）题目4（6）
640 / 3847Juruoer130:39:050:02:510:20:140:39:05

题目及解答

统计星号

2315. 统计星号

给你一个字符串 s ，每 两个 连续竖线 '|' 为 一对 。换言之，第一个和第二个 '|' 为一对，第三个和第四个 '|' 为一对，以此类推。

请你返回 不在 竖线对之间，s 中 '*' 的数目。

注意，每个竖线 '|' 都会 恰好 属于一个对。

提示：

  • 1 <= s.length <= 1000
  • s 只包含小写英文字母，竖线 '|' 和星号 '*' 。
  • s 包含 偶数 个竖线 '|' 。

示例一：

输入：s = “l|*e*et|c**o|*de|”
输出：2
解释：不在竖线对之间的字符加粗加斜体后，得到字符串：“l|*e*et|c**o|*de|” 。
第一和第二条竖线 ‘|’ 之间的字符不计入答案。
同时，第三条和第四条竖线 ‘|’ 之间的字符也不计入答案。
不在竖线对之间总共有 2 个星号，所以我们返回 2 。

示例二：

输入：s = “iamprogrammer”
输出：0
解释：在这个例子中，s 中没有星号。所以返回 0 。

示例三：

输入：s = “yo|uar|e**|b|e***au|tifu|l”
输出：5
解释：需要考虑的字符加粗加斜体后：“yo|uar|e**|b|e***au|tifu|l” 。不在竖线对之间总共有 5 个星号。所以我们返回 5 。

解决方案：

模拟：

使用一个标记来判断当前字符是否在一对 '|' 之中。可以发现，每遇到一个 '|' ，标记取反。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution
{
public:
    int countAsterisks(string s)
    {
        bool flag = true;
        int rst = 0;
        for(char c : s)
        {
            if(c == '|')
            {
                flag = !flag;
                continue;
            }
            if(flag && c == '*')
                ++rst;
        }
        return rst;
    }
};

时间复杂度：O(n)O(n) ；空间复杂度：O(1)O(1) 。 n 为 s 长度。

统计无向图中无法互相到达点对数

2316. 统计无向图中无法互相到达点对数

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

请你返回 无法互相到达 的不同 点对数目 。

提示：

  • 1 <= n <= 1e5
  • 0 <= edges.length <= 2 * 1e5
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • 不会有重复边。

示例一：

示例一图

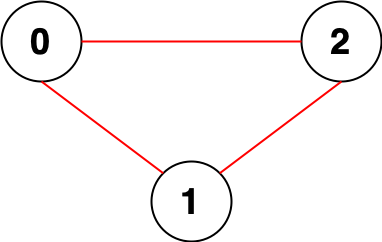
输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。

示例二：

示例二图

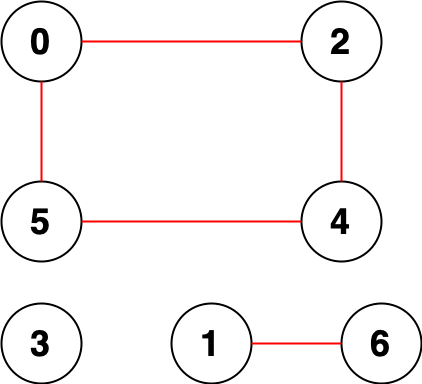
输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。

解决方案：

并查集：

利用并查集计算出所有连通图的节点个数，根据数学的排列组合知识即可计算出无法相互到达的点对数。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution
{
private:
    vector<int> root; // 记录每个节点的根节点

    int find(int x) // 查找节点 x 的根节点，利用递归来压缩路径
    {
        if (root[x] != x)
            root[x] = find(root[x]);
        return root[x];
    }

public:
    long long countPairs(int n, vector<vector<int>> &edges)
    {
        long long rst = 0;
        root.resize(n);
        int have[n]; // 记录每个根节点的连通图的节点数
        int i;
        
        // 初始时假设所有节点都孤立，每个点的根节点是其自己
        for (i = 0; i < n; ++i)
        {
            root[i] = i;
            have[i] = 1;
        }
        
        // 根据给定的边将各点连通
        for (auto &x : edges)
        {
            int r1 = find(x[0]);
            int r2 = find(x[1]);
            
            // 如果 r1 和 r2 之前不属于同一个连通图，但它们之间有边，将 r2 的连通图加入到 r1 的连通图里
            if(r1 != r2)
            {
                root[r2] = r1;
                have[r1] += have[r2];
                have[r2] = 0;
            }
        }
        
        // 根据数学排列组合的知识可知，结果要求无法相互到达的点对，即计算每所有 两两不同的连通图的节点数的乘积 的和，我们可以按照一个顺序遍历所有的连通图，并用 other 来统计未遍历的连通图的节点总数，那么对于每个遍历到的连通图，计算其节点数与当前未遍历到的连通图的节点数的乘积，并求和，即可以无重复的计算出所有无法到达的点对数。
        int other = n; // 当前未遍历到的连通图的节点总数
        for (i = 0; i < n; ++i)
        {
            if(have[i]) // 如果 i 是一个连通图的根，have[i] 就是该连通图的节点个数
            {
                other -= have[i];
                rst += (1LL * have[i] * other);
            }
        }
        return rst;
    }
};

时间复杂度：O(n)O(n) ；空间复杂度：O(n)O(n) 。n 为节点个数。

操作后的最大异或和

2317. 操作后的最大异或和

给你一个下标从 0 开始的整数数组 nums 。一次操作中，选择 任意 非负整数 x 和一个下标 i ，更新 nums[i] 为 nums[i] AND (nums[i] XOR x) 。

注意，AND 是逐位与运算，XOR 是逐位异或运算。

请你执行 任意次 更新操作，并返回 nums 中所有元素 最大 逐位异或和。

提示：

  • 1 <= nums.length <= 1e5
  • 0 <= nums[i] <= 1e8

示例一：

输入：nums = [3,2,4,6]
输出：7
解释：选择 x = 4 和 i = 3 进行操作，num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2 。
现在，nums = [3, 2, 4, 2] 且所有元素逐位异或得到 3 XOR 2 XOR 4 XOR 2 = 7 。
可知 7 是能得到的最大逐位异或和。
注意，其他操作可能也能得到逐位异或和 7 。

示例二：

输入：nums = [1,2,3,9,2]
输出：11
解释：执行 0 次操作。
所有元素的逐位异或和为 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11 。
可知 11 是能得到的最大逐位异或和。

解决方案：

位运算 (脑筋急转弯) ：

根据位运算的特点，我们可以发现：

  • 对于一个已有的非负整数 num 和 任意一个 期望获得的非负整数 target ，我们都可以选择出一个非负整数 x ，使得 num XOR x = target 。
  • 对于一个已有的非负整数 num ，对于 num 的二进制中 任意一个 为 1 的位 idx，我们都可以选择出一个非负整数 x，进行操作 num = num AND x 后， num 的二进制中第 idx 位的 1 变为 0 ，而不改变 num 的二进制中其他位的值。

所以对于题设给出的操作，相当于选出 nums[i] 中的某个元素 num，将 num 的二进制中的某个为 1 的位变为 0。而要使得 nums 中所有元素的异或和最大，只需要将所有元素的二进制排列出来，若某一位，有至少一个元素的二进制在该位为 1，则需要操作这些元素，使得该位为 1 的元素的个数为奇数，那么所有元素的异或和在该位即是 1，最终异或和最大。

对于二进制的第 idx 位，若存在某一个元素该位为 1，那么操作后最大的异或和在该位也为 1 ，若所有元素的二进制在该位均为 0，那么最大异或和在该位为 0。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution
{
public:
    int maximumXOR(vector<int> &nums)
    {
        int have[27]; // have[i] 是否有元素的二进制在第 i 位为 1，初始时每一位都没有
        memset(have, 0, sizeof(have));
        int i, j;
        for(int x : nums)
        {
            i = 0;
            while(x) // 遍历 x 的二进制位
            {
                if(x & 1) // 该位为 1
                    have[i] = 1;
                x >>= 1;
                ++i;
            }
        }
        int rst = 0;
        
        // 计算最大异或和
        for (i = 26; i > -1; --i)
        {
            rst <<= 1;
            rst += have[i];
        }
        return rst;
    }
};

时间复杂度：O(c×n)O(c \times n) ；空间复杂度：O(c)O(c)，c 为二进制的位数，本题数字范围限定 c 为 28 ，n 为 nums 的长度。

位运算优化：

更进一步，我们发现遍历所有元素的二进制，并记录出存在 1 的位这件事本身不就是 按位或 运算吗？所以我们只需要将所有元素按位或即可得出答案！

代码：

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int maximumXOR(vector<int>& nums) {
        int rst = 0;
        for(int num : nums)
            rst |= num;
        return rst;
    }
};

时间复杂度：O(n)O(n) ；空间复杂度：O(1)O(1) 。

不同骰子序列的数目

2318. 不同骰子序列的数目

给你一个整数 n 。你需要掷一个 6 面的骰子 n 次。请你在满足以下要求的前提下，求出 不同 骰子序列的数目：

  1. 序列中任意 相邻 数字的 最大公约数 为 1 。
  2. 序列中 相等 的值之间，至少有 2 个其他值的数字。正式地，如果第 i 次掷骰子的值 等于 第 j 次的值，那么 abs(i - j) > 2 。

请你返回不同序列的 总数目 。由于答案可能很大，请你将答案对 1e9 + 7 取余 后返回。

如果两个序列中至少有一个元素不同，那么它们被视为不同的序列。

提示：

  • 1 <= n <= 1e4

示例一：

输入：n = 4
输出：184
解释：一些可行的序列为 (1, 2, 3, 4) ，(6, 1, 2, 3) ，(1, 2, 3, 1) 等等。
一些不可行的序列为 (1, 2, 1, 3) ，(1, 2, 3, 6) 。
(1, 2, 1, 3) 是不可行的，因为第一个和第三个骰子值相等且 abs(1 - 3) = 2 （下标从 1 开始表示）。
(1, 2, 3, 6) i是不可行的，因为 3 和 6 的最大公约数是 3 。
总共有 184 个不同的可行序列，所以我们返回 184 。

示例二：

输入：n = 2
输出：22
解释：一些可行的序列为 (1, 2) ，(2, 1) ，(3, 2) 。
一些不可行的序列为 (3, 6) ，(2, 4) ，因为最大公约数不为 1 。
总共有 22 个不同的可行序列，所以我们返回 22 。

解决方案：

动态规划：

dp[k][i][j] 表示直到第 k 次投骰子，投到的是 i，且前一次投骰子投到的是 j 的序列数，且仅当 i 和 j 互质时才有意义

按照题意很容易可以得出：

  • 当 k == 2 时，在 k = 1 次投骰子结果确定的情况下，仅有一种可能 (感觉在说废话) 。 dp[2][i][j] = 1 （j 与 i 互质）。

  • 当 k > 2 时，需要取出第 k - 1 次投骰子结果为 j 且第 k - 2 次投骰子结果与 i 不同是所有结果， dp[k][i][j] = Σ(dp[k - 1][j][r])，r 从 1 到 6，i 与 j 互质，j 与 r 互质，i != r 。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution
{
public:
    int distinctSequences(int n)
    {
        if(n == 1)
            return 6;

        int i, j, k, r, MOD = 1e9 + 7;
        // dp[k][i][j] 表示直到第 k 次投骰子，投到的是 i，且前一次投骰子投到的是 j 的序列数，且仅当 i 和 j 互质时才有意义
        // 当 k > 2 时，dp[k][i][j] = Σ(dp[k - 1][j][r])，r 从 1 到 6，i 与 j 互质，j 与 r 互质，i != r
        // 当 k == 2 时，dp[2][i][j] = 1 （j 与 i 互质）
        int dp[n + 1][7][7];
        memset(dp, 0, sizeof(dp));
        
        // hz[i] 表示和 i 互质的数
        vector<vector<int>> hz = {
            {},
            {2, 3, 4, 5, 6},
            {1, 3, 5},
            {1, 2, 4, 5},
            {1, 3, 5},
            {1, 2, 3, 4, 6},
            {1, 5}
        };

        // k == 2 时特殊处理
        for (i = 1; i < 7; ++i)
        {
            for(auto j : hz[i]) // j 必须和 i 互质
                dp[2][i][j] = 1;
        }
        
        for (k = 3; k <= n; ++k)
        {
            for (i = 1; i < 7; ++i)
            {
                for (auto j : hz[i]) // j 必须和 i 互质
                {
                    for(auto r : hz[j]) // r 必须和 j 互质
                    {
                        if(i == r) // r 不能和 i 相同
                            continue;
                        dp[k][i][j] = (dp[k][i][j] + dp[k - 1][j][r]) % MOD;
                    }
                }
            }
        }

        int rst = 0;
        for (i = 1; i < 7; ++i)
        {
            for(auto j : hz[i])
                rst = (rst + dp[n][i][j]) % MOD;
        }
        
        return rst;
    }
};

时间复杂度：O(n×c3)O(n \times c^3) ； 空间复杂度：O(n×c2)O(n \times c^2)。其中 c 表示骰子点数范围，本题为 6。