凸包问题-Andrew算法

一、前言

在做前两天LeetCode上的每日一题587.安装栅栏时发现这是一道之前都没有见过的题型（我平常也很少主动刷一些几何类的题），看了评论后发现这就是之前略有耳闻的凸包问题，但是一直没有去研究，既然现在遇到了就解决它吧！

在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点( $X_1$ ，… $X_n$ )的凸组合来构造（听的不是很懂）。其实就好比在一块木板上钉了若干钉子，现在用一根橡皮筋将所有钉子包起（钉子必须在橡皮筋内），这个橡皮筋所经过的所有钉子就是这若干钉子的凸包。看下面的题目描述也许更容易理解。

解决凸包问题常见的有三种算法，分别是Jarvis算法（时间复杂度O( $n^2$ )）、Graham算法（时间复杂度O( $n\log(n)$ )）和Andrew算法（时间复杂度O( $n\log(n)$ ），这里只介绍Andrew算法（Ps：建议也了解一下前两种算法）。

二、题目描述

我们直接以安装栅栏这道题为例：

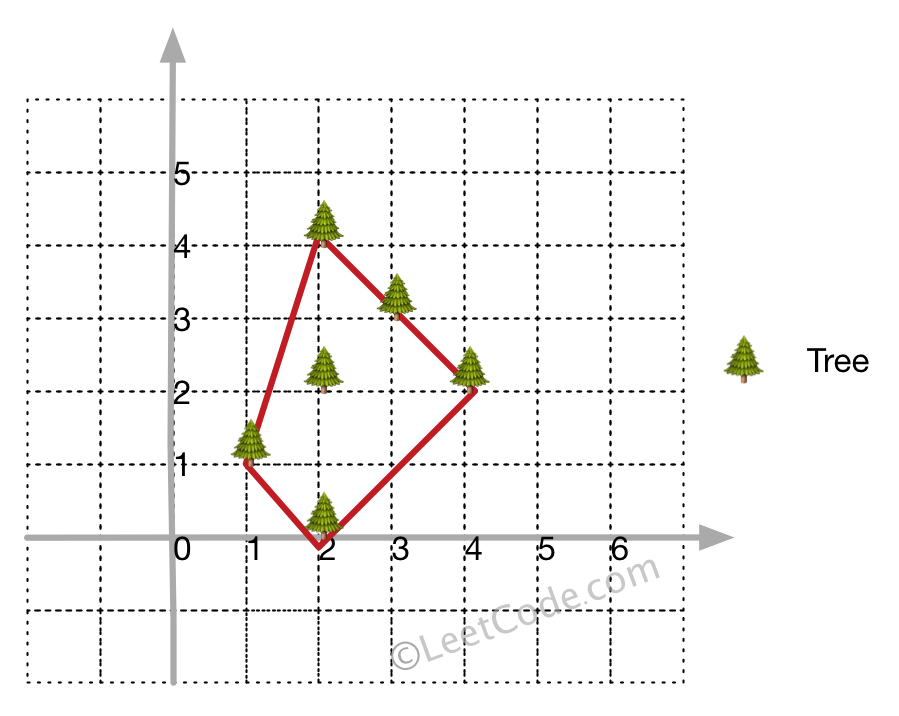
在一个二维的花园中，有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵，你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时，花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。
输入: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
输出: [[1,1],[2,0],[4,2],[3,3],[2,4]]
解释:
注意:
所有的树应当被围在一起。你不能剪断绳子来包围树或者把树分成一组以上。
输入的整数在 0 到 100 之间。
花园至少有一棵树。
所有树的坐标都是不同的。
输入的点没有顺序。输出顺序也没有要求。

三、解决方案

1、基本原理

我们仔细观察X的凸包S（假设S中各个点按照逆时针进行排序，例如上述示例中的输出序列的顺序），可以发现，对于S上的任意相邻的两点 p、q 有，X上的所有点均位于向量 $\vec{pq}$ （假设最后一个点的下一个点是第一个点）的左侧（或在这个向量所在的直线上），也就是说我们要找到这样一个点序列S，X中的所有点均在S中相邻的两个点形成的向量（由前一个点指向后一个点）的左侧（或在这个向量所在的直线上）。

2、前置知识

如何判断一个点 r 在向量 $\vec{pq}$ 的左边还是右边呢？答案是计算 $\vec{pq}$ 和 $\vec{qr}$ 的叉积。

若向量 $\vec{pq}$ 和向量 $\vec{qr}$ 的叉积为正，则 r 在 $\vec{pq}$ 的左边，为负则 r 在 $\vec{pq}$ 的右边，为0则说明 p、q、r 共线.

叉积计算公式：

$\begin{aligned} cross(p, q, r) &= \vec{pq} × \vec{qr} \\ &= \begin{vmatrix} (q_{x} - p_{x} ) & (q_{y} - p_{y}) \\ (r_{x} - q_{x}) & (r_{y} - q_{y}) \end{vmatrix} \\ &= (q_{x} - p_{x} ) \times (r_{y} - q_{y}) - (q_{y} - p_{y}) \times (r_{x} - q_{x}) \end{aligned}$

即：

int cross(const vector<int> &p, const vector<int> &q, const vector<int> &r)
{
    return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0]);
}

3、Andrew算法

那么应当以一种怎样的顺序来考察点集X中的各个点，以判断其是否属于凸包S呢？其实这也就是各种的凸包算法的不同之处。

Andrew的办法是将所有的点按照x坐标从小到大排序，若x坐标相同则按y坐标从小到大排序，设排序后的点集为sortX，按照凸包的定义可以知道x坐标最小的点也就是sortX[0]一定属于凸包。

我们再定义一个栈stack，这个栈里存放目前假定的凸包，自左向右遍历sortX，对取出的每一个点 r，做如下操作：

若栈中元素个数少于2，直接将r入栈，遍历下一个元素，否则进入2。
取出栈中倒数第二个元素 p 和最后一个元素 q ，那么若cross(p, q, r)小于0，说明 r 位于 $\vec{pq}$ 的右边，则 q 不满足凸包的定义（若q属于凸包，所有的点都应当在 $\vec{pq}$ 的左边），将 q 出栈，进入1，否则将r入栈，遍历下一个元素。

此番遍历后凸包的下半部分就计算完成了：

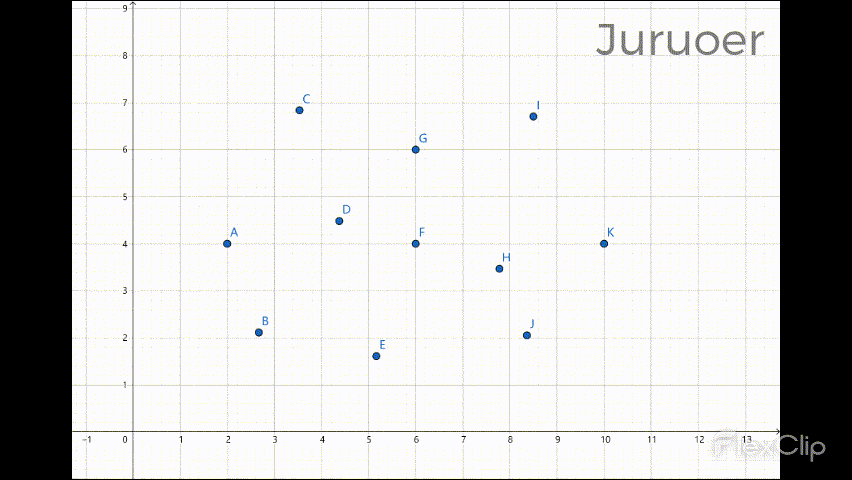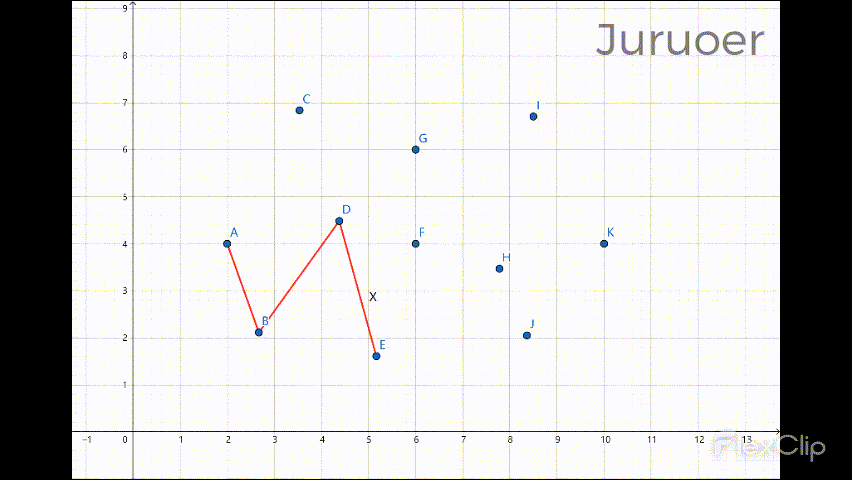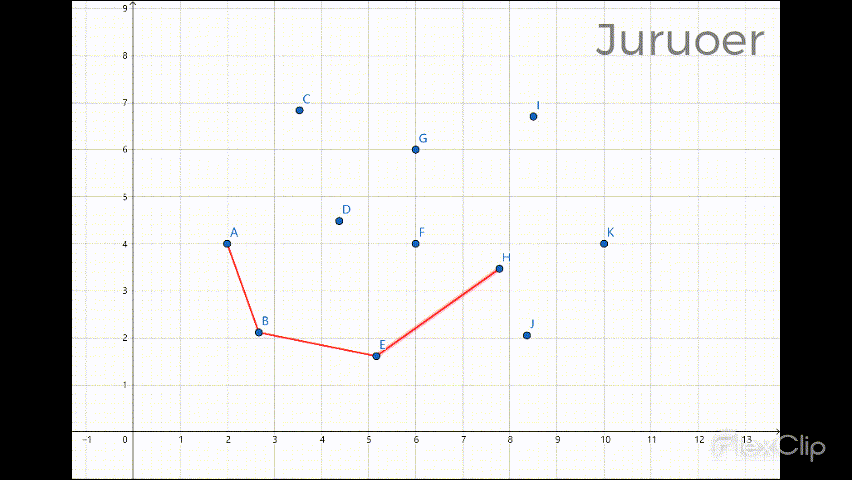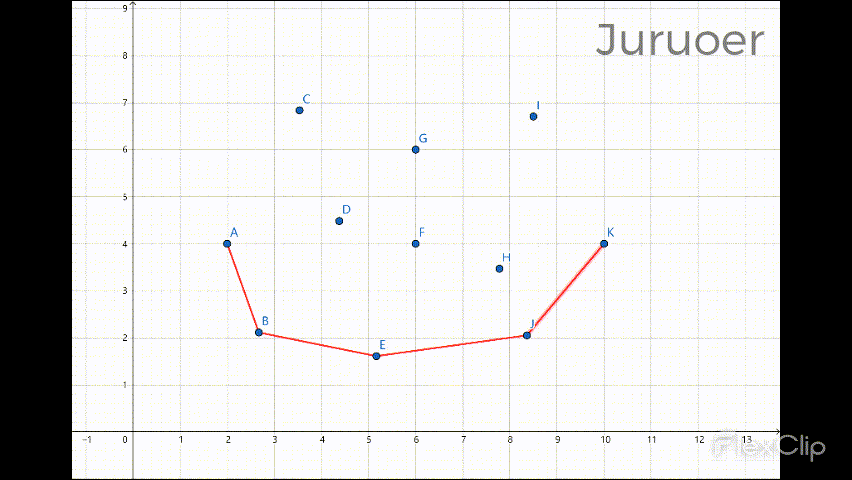
设此时栈中有size个元素，我们再自右向左遍历sortX（最右边的点不用再遍历了），对取出的每一个点 r，做如下操作：

若该点已经存在于下半区了，跳过该点，遍历下一个元素，否则进入2。
若栈中元素个数少于m + 1，直接将r入栈，遍历下一个元素，否则进入3。
取出栈中倒数第二个元素 p 和最后一个元素 q ，那么若cross(p, q, r)小于0，说明 r 位于 $\vec{pq}$ 的右边，则 q 不满足凸包的定义，将 q 出栈，进入2，否则将r入栈，遍历下一个元素。

此番遍历后凸包的上半部分就计算完成了：

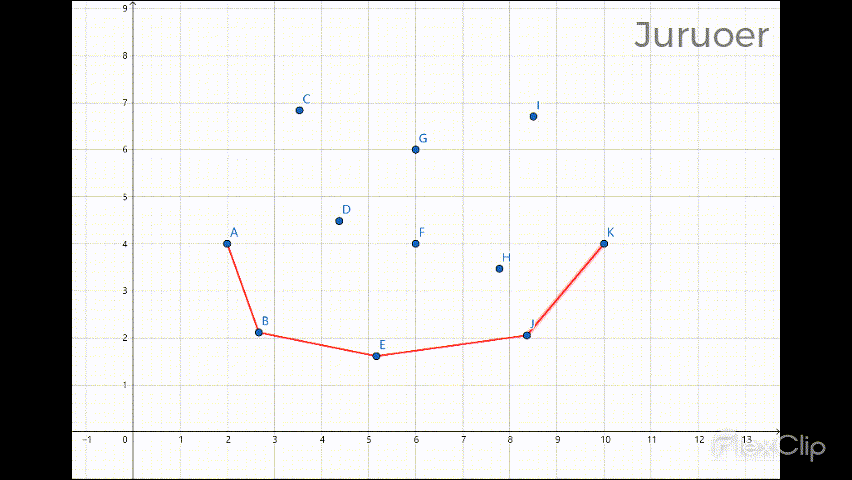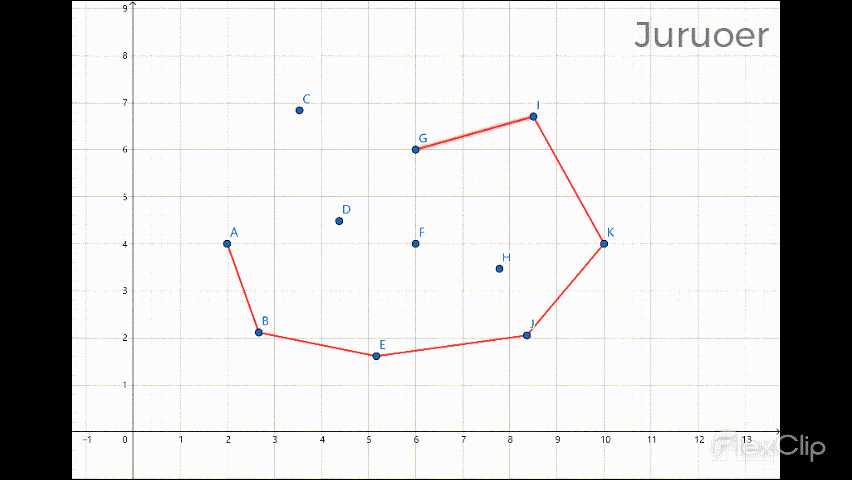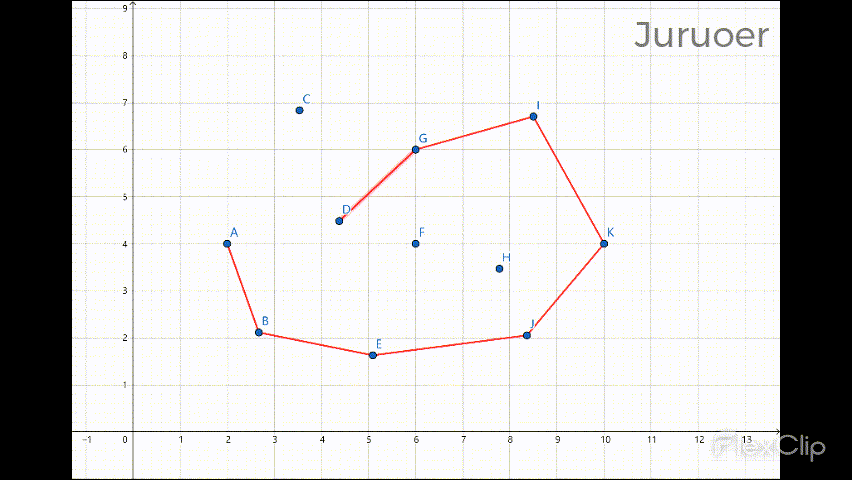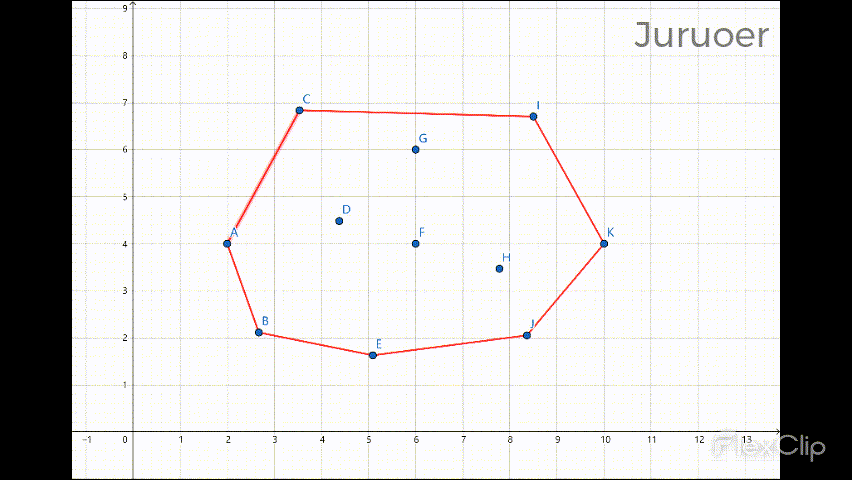
综上，我们可以写出Andrew算法的代码：

vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
    //我们以安装栅栏为例，每棵树就是一个点
    int i, n = trees.size();
    if(n < 4)//当点集X的点的个数少于4个的话，则点集X中所有点都属于凸包
        return trees;
    sort(trees.begin(), trees.end(), [](const vector<int> &a, const vector<int> &b) {
        if(a[0] == b[0])
            return a[1] < b[1];
        return a[0] < b[0]; 
    });//按坐标的x值的大小进行排序（从小到大），若x值相同则按y值大小排序（从小到大）
    vector<int> hull;//单调栈（按照向量的叉积）
    vector<bool> used(n, false);//记录下半区已经使用过的点
    hull.emplace_back(0);//第一个点不用记录，因为计算上半区时需要计算这个点
    for (i = 1; i < n; ++i)//计算下半区
    {
        while(hull.size() > 1 && cross(trees[hull[hull.size() - 2]], trees[hull.back()], trees[i]) < 0)
        {// 当前点在右边
            used[hull.back()] = false;
            hull.pop_back();
        }
        used[i] = true;
        hull.emplace_back(i);
    }
    int m = hull.size();//下半区的点的个数
    for (i = n - 2; i > -1; --i)//计算上半区
    {
        if(used[i])
            continue;
        while (hull.size() > m &&cross(trees[hull[hull.size() - 2]], trees[hull.back()], trees[i]) < 0)
            hull.pop_back();//此处为何不需要将used[i]置为false？因为之后再也不会使用到used[i]了
        hull.emplace_back(i);
    }
    hull.pop_back();//第一个点重复入栈了，对于第一个点，既然其一定是在凸包中的，那么为什么计算上半区时需要遍历第一个点呢？如果不遍历的话，此处还可以少一步退栈，岂不是更方便？其实你可以试试上面的gif图给出的例子，看看计算上半区时不考虑第一个点会有什么错误。
    vector<vector<int>> rst;
    for(int &x : hull)
        rst.emplace_back(trees[x]);
    return rst;
}