非常遗憾，本次周赛仅写出前两题。

战局详情

排名用户名得分完成时间题目1（3）题目2（5）题目3（5）题目4（6）
1553 / 5915Juruoer80:32:120:12:350:32:12

题目及解答

计算应缴税款总额

5259. 计算应缴税款总额

给你一个下标从 0 开始的二维整数数组 brackets ，其中 brackets[i] = [upperi, percenti] ，表示第 i 个税级的上限是 upperi ，征收的税率为 percenti 。税级按上限 从低到高排序（在满足 0 < i < brackets.length 的前提下，upperi-1 < upperi ）。

税款计算方式如下：

  • 不超过 upper0 的收入按税率 percent0 缴纳
  • 接着 upper1 - upper0 的部分按税率 percent1 缴纳
  • 然后 upper2 - upper1 的部分按税率 percent2 缴纳
  • 以此类推

给你一个整数 income 表示你的总收入。返回你需要缴纳的税款总额。与标准答案误差不超 1e-5 的结果将被视作正确答案。

提示：

  • 1 <= brackets.length <= 100
  • 1 <= upperi <= 1000
  • 0 <= percenti <= 100
  • 0 <= income <= 1000
  • upperi 按递增顺序排列
  • upperi 中的所有值 互不相同
  • 最后一个税级的上限大于等于 income

示例一：

输入：brackets = [[3,50],[7,10],[12,25]], income = 10
输出：2.65000
解释：
前 $3 的税率为 50% 。需要支付税款 $3 * 50% = $1.50 。
接下来 $7 - $3 = $4 的税率为 10% 。需要支付税款 $4 * 10% = $0.40 。
最后 $10 - $7 = $3 的税率为 25% 。需要支付税款 $3 * 25% = $0.75 。
需要支付的税款总计 $1.50 + $0.40 + $0.75 = $2.65 。

示例二：

输入：brackets = [[1,0],[4,25],[5,50]], income = 2
输出：0.25000
解释：
前 $1 的税率为 0% 。需要支付税款 $1 * 0% = $0 。
剩下 $1 的税率为 25% 。需要支付税款 $1 * 25% = $0.25 。
需要支付的税款总计 $0 + $0.25 = $0.25 。

示例三：

输入：brackets = [[2,50]], income = 0
输出：0.00000
解释：
没有收入，无需纳税，需要支付的税款总计 $0 。

解决方案：

模拟：

将 income 按照 brackets 分为若干份，并根据每份的税率计算相应的税收。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution
{
public:
    double calculateTax(vector<vector<int>> &brackets, int income)
    {
        double rst = 0;
        double pre = 0; // 之前的税率所覆盖的收入范围：[0, pre]。
        for (int i = 0; i < brackets.size(); ++i)
        {
            // 税率为 brackets[i][1] / 100 的收入范围为：[pre, min(brackets[i][0], income)]
            rst += (min(brackets[i][0], income) - pre) * brackets[i][1] / 100;
            // 收入太少了，之后的税雨你无瓜(扎心)
            if(income <= brackets[i][0])
                break;
            pre = brackets[i][0];
        }
        return rst;
    }
};

时间复杂度为：O(n)O(n) ；空间复杂度为：O(1)O(1) 。其中 n 表示 brackets 的长度。

网格中的最小路径代价

5270. 网格中的最小路径代价

给你一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1) 中的任何一个单元格。注意： 在最后一行中的单元格不能触发移动。

每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m * n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。

grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 50
  • grid 由从 0 到 m * n - 1 的不同整数组成
  • moveCost.length == m * n
  • moveCost[i].length == n
  • 1 <= moveCost[i][j] <= 100

示例一：

示例一图

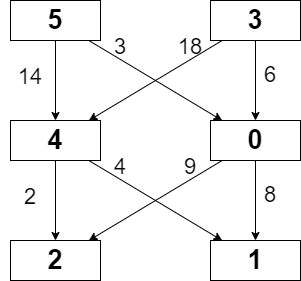
输入：grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出：17
解释：最小代价的路径是 5 -> 0 -> 1 。

  • 路径途经单元格值之和 5 + 0 + 1 = 6 。
  • 从 5 移动到 0 的代价为 3 。
  • 从 0 移动到 1 的代价为 8 。

路径总代价为 6 + 3 + 8 = 17 。

示例二：

输入：grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出：6
解释：
最小代价的路径是 2 -> 3 。

  • 路径途经单元格值之和 2 + 3 = 5 。
  • 从 2 移动到 3 的代价为 1 。

路径总代价为 5 + 1 = 6 。

解决方案：

动态规划：

若 grid 有 m 行 n 列。

设 dp[i][j] 表示第 i 行第 j 列的元素到达最后一行的最小路径代价，则：

dp[i][j] = grid[i][j] + min(dp[i + 1][k] + moveCost[grid[i][j]][k]) ，其中 k 由 0 到 n - 1 ；

dp[m - 1][j] = grid[m - 1][j] 。

我们可以直接使用 grid 来代替 dp。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution
{
public:
    int minPathCost(vector<vector<int>> &grid, vector<vector<int>> &moveCost)
    {
        int m = grid.size();
        int n = grid[0].size();
        int i, j, k;
        int cost;
        // 由倒数第二行计算到第一行，最后一行已经保存在 grid 中了
        for (i = m - 2; i > -1; --i)
        {
            // 计算第 i 行第 j 列的元素到达最后一行的最小路径代价
            for (j = 0; j < n; ++j)
            {
                cost = 0x7fffffff;
                for (k = 0; k < n; ++k)
                {
                    // 由 grid[i][j] 移动到 grid[i + 1][k]
                    cost = min(cost, grid[i + 1][k] + moveCost[grid[i][j]][k]);
                }
                grid[i][j] += cost;
            }
        }
        // 返回最小代价
        return *min_element(grid.at(0).begin(), grid.at(0).end());
    }
};

时间复杂度为：O(m×n2)O(m \times n^2) ；空间复杂度为：O(1)O(1) 。其中 m 、n 分别为 grid 的行数和列数。

公平分发饼干

5289. 公平分发饼干

给你一个整数数组 cookies ，其中 cookies[i] 表示在第 i 个零食包中的饼干数量。另给你一个整数 k 表示等待分发零食包的孩子数量，所有 零食包都需要分发。在同一个零食包中的所有饼干都必须分发给同一个孩子，不能分开。

分发的 不公平程度 定义为单个孩子在分发过程中能够获得饼干的最大总数。

返回所有分发的最小不公平程度。

提示：

  • 2 <= cookies.length <= 8
  • 1 <= cookies[i] <= 1e5
  • 2 <= k <= cookies.length

示例一：

输入：cookies = [8,15,10,20,8], k = 2
输出：31
解释：一种最优方案是 [8,15,8] 和 [10,20] 。

  • 第 1 个孩子分到 [8,15,8] ，总计 8 + 15 + 8 = 31 块饼干。
  • 第 2 个孩子分到 [10,20] ，总计 10 + 20 = 30 块饼干。

分发的不公平程度为 max(31,30) = 31 。
可以证明不存在不公平程度小于 31 的分发方案。

示例二：

输入：cookies = [6,1,3,2,2,4,1,2], k = 3
输出：7
解释：一种最优方案是 [6,1]、[3,2,2] 和 [4,1,2] 。

  • 第 1 个孩子分到 [6,1] ，总计 6 + 1 = 7 块饼干。
  • 第 2 个孩子分到 [3,2,2] ，总计 3 + 2 + 2 = 7 块饼干。
  • 第 3 个孩子分到 [4,1,2] ，总计 4 + 1 + 2 = 7 块饼干。

分发的不公平程度为 max(7,7,7) = 7 。
可以证明不存在不公平程度小于 7 的分发方案。

解决方案：

一、回溯 + 枝剪：

利用递归计算所有的零食分发方式，并计算出最小的不公平程度。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution
{
public:
    // have[i] 表示第 i 个小朋友获得的零食数
    vector<int> cooks, have;
    int n, c, rst, idx;

    // idx 表示分发到第 idx 包零食
    void dfs()
    {
        if(idx == n) // 零食分发完了
        {
            // 计算所有小朋友获得的零食数的最大值（即此情况下的不公平程度），与 rst 比较
            rst = min(rst, *max_element(have.begin(), have.end()));
            return;
        }

        for (int i = 0; i < c; ++i)
        {
            // 将第 idx 包零食分给第 i 个小朋友
            have[i] += cooks[idx];
            if(have[i] < rst) // 枝剪，若这个小朋友的零食已经比之前的分配方法得出的不公平程度大，则不需要继续计算了
            {
                ++idx;
                dfs();
                --idx;
            }
            // 再给他拿回来(have 是所有递归共用的)
            have[i] -= cooks[idx];
        }
    }

    int distributeCookies(vector<int> &cookies, int k)
    {
        cooks = cookies;
        n = cookies.size();
        c = k;
        rst = 0x7fffffff;
        have.resize(k, 0);
        idx = 0;
        dfs();
        return rst;
    }
};

所有零食的分发方法共有knk ^ n 种，递归总次数为knk ^ n。故时间复杂度为：O(kn)O(k^n) ； 空间复杂度为：O(n+kn)O(n + k ^ n) 。其中 n 表示零食的包数，k 表示小朋友的数量。其实枝剪后时间复杂度和空间复杂度远远低于O(kn)O(k ^ n)。

二、动态规划 + 状态压缩：

因为最多有 8 包零食，故可以将零食的组合状态压缩为：零食集合 k ，其含义为： k 的二进制中若第 idx 位（自右向左，自 0 开始）为 1，则表示第 idx 包零食属于该零食集合。易知一共有 1 << n 种零食集合。

设 dp[i][j] 表示前 i 个小朋友分得的零食集合为 j 时的最小不公平程度。

则 dp[i][j] = min(max(dp[i - 1][j \ s], sum[s]))，其中，s 表示第 i 位小朋友获得的零食集合，且 s 必须为 j 的子集，j \ s 表示集合 j 去除集合 s 的集合，sum[s] 表示集合 s 的零食数量之和。

因为 s 为 j 的子集，故 j \ s = j ^ s ， 另外，可以发现 sum[s] = dp[0][s]。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution
{
public:
    int distributeCookies(vector<int> &cookies, int k)
    {
        int n = cookies.size();
        int N = 1 << n;
        // 对于零食集合 k，k 的二进制中若第 idx 位（自右向左，自 0 开始）为 1，则表示第 idx 包零食属于该零食集合。
        // dp[i][j] 表示前 i 个小朋友分得的零食集合为 j 时的最小不公平程度。
        // dp[i][j] = min(max(dp[i - 1][j \ s], sum[s]))，s 表示第 i 位小朋友获得的零食集合，且 s 必须为 j 的子集，j \ s 表示集合 j 去除集合 s 的集合，sum[s] 表示集合 s 的零食数量之和。
        // 因为 s 为 j 的子集，故 j \ s = j ^ s, 另外，可以发现 sum[s] = dp[0][s]。
        // 可知一共有 1 << n 种零食集合
        int dp[k][N];
        memset(dp, 0x7f, sizeof(dp)); // 初始化 dp 每个元素为 0x7f7f7f7f > 8 * 10^5
        int i, j, s;

        // 初始化 只有一位小朋友时的情况 dp[0][j]，也即 sum[j]
        for (j = 0; j < N; ++j)
        {
            dp[0][j] = 0;
            // 遍历所有零食
            for (i = 0; i < n; ++i)
            {
                // 若该零食属于集合 j
                if(j & (1 << i))
                    dp[0][j] += cookies[i];
            }
        }

        // 计算有 i + 1 位小朋友时的情况
        for (i = 1; i < k; ++i)
        {
            dp[i][0] = 0;
            // 对于集合 j
            for (j = 1; j < N; ++j)
            {
                // 若 s 为 j 的子集，则 s <= j
                for (s = 0; s <= j; ++s)
                {
                    // 当 s 为 j 的子集时，尝试更新 dp[i][j]
                    if(s | j <= j)
                        dp[i][j] = min(dp[i][j], max(dp[i - 1][j ^ s], dp[0][s]));
                }
            }
        }
        return dp[k - 1][N - 1];
    }
};

时间复杂度为：O(n×2n+k×∑i=12ni)=O(n×2n+4n)O(n \times 2 ^ n + k \times \sum_{i = 1} ^{2 ^ n} i) = O(n \times 2 ^ n + 4 ^ n) ；空间复杂度为：O(k×2n)O(k \times 2 ^ n) 。其中 n 表示零食的包数，k 表示小朋友的个数。

公司命名

6094. 公司命名

给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下：

  • 从 ideas 中选择 2 个 不同 名字，称为 ideaA 和 ideaB 。
  • 交换 ideaA 和 ideaB 的首字母。
  • 如果得到的两个新名字 都 不在 ideas 中，那么 ideaA ideaB（串联 ideaA 和 ideaB ，中间用一个空格分隔）是一个有效的公司名字。
  • 否则，不是一个有效的名字。

返回 不同 且有效的公司名字的数目。

提示：

  • 2 <= ideas.length <= 5 * 1e4
  • 1 <= ideas[i].length <= 10
  • ideas[i] 由小写英文字母组成
  • ideas 中的所有字符串 互不相同

示例一：

输入：ideas = [“coffee”,“donuts”,“time”,“toffee”]
输出：6
解释：下面列出一些有效的选择方案：

  • (“coffee”, “donuts”)：对应的公司名字是 “doffee conuts” 。
  • (“donuts”, “coffee”)：对应的公司名字是 “conuts doffee” 。
  • (“donuts”, “time”)：对应的公司名字是 “tonuts dime” 。
  • (“donuts”, “toffee”)：对应的公司名字是 “tonuts doffee” 。
  • (“time”, “donuts”)：对应的公司名字是 “dime tonuts” 。
  • (“toffee”, “donuts”)：对应的公司名字是 “doffee tonuts” 。
    因此，总共有 6 个不同的公司名字。

下面列出一些无效的选择方案：

  • (“coffee”, “time”)：在原数组中存在交换后形成的名字 “toffee” 。
  • (“time”, “toffee”)：在原数组中存在交换后形成的两个名字。
  • (“coffee”, “toffee”)：在原数组中存在交换后形成的两个名字。

示例二：

输入：ideas = [“lack”,“back”]
输出：0
解释：不存在有效的选择方案。因此，返回 0 。

解决方案：

哈希 + 枚举 + 分组：

对于每个被选出作为 ideaA 的字符串，若将其首字母（假设为 c1）变为 c2 后不存在于 ideas 中，则 ideas 中所有首字母为 c2 且将首字母变为 c1 后不存在于 ideas 中的所有字符串均是有效的 ideaB。

事实上，我们可以先计算出 ideas 中的所有字符串其改变首字母后是否存在于 ideas 中，且将首字母由相同字符转化为另一相同字符后不存在于 ideas 中的字符串作为一组，并统计各组的字符串个数，保存至 cnts 中，即：

设 cnts[i][j] 表示 ideas 中首字母为 i + 'a' 且将首字母变为 j + 'a' 时产生的新字符串不在 ideas 中的字符串个数。

那么对于所有的 ideaA，如果他的首字母（假设为 to + 'a'）变为 j + 'a'，那么合理的 ideaB 的个数为 cnts[j][to] 。

对于某个因为改变了首字母而得到的字符串，可以使用哈希表来更快的判断其是否存在于 ideas 中。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution
{
public:
    long long distinctNames(vector<string> &ideas)
    {
        // 使用哈希表可以更快的比较出某个新字符串是否存在于 ideas 中
        unordered_set<string> theSet;
        int i, j, n = ideas.size();

        // cnts[i][j] 表示 ideas 中首字母为 i + 'a' 且 将首字母变为 j + 'a' 时产生的新字符串不在 ideas 中的字符串个数
        int cnts[26][26];

        // flag[i][j] == true 表示 ideas[i] 的首字母变为 j + 'a' 时产生的新字符串不在 ideas 中
        bool flags[n][26];

        memset(cnts, 0, sizeof(cnts));
        memset(flags, false, sizeof(flags));

        for(string &idea : ideas)
            theSet.emplace(idea);

        int ori;
        string temp;
        for (i = 0; i < n; ++i)
        {
            temp = ideas[i];
            ori = temp[0] - 'a'; // ideas[i] 原来的首字母
            // 遍历新的首字母
            for (j = 0; j < 26; ++j)
            {
                // 构建新字符串
                temp[0] = j + 'a';
                // 若新字符串不存在于 ideas 中
                if(theSet.count(temp) == 0)
                {
                    flags[i][j] = true;
                    ++cnts[ori][j];
                }
            }
        }

        long long rst = 0;
        int to;

        // 遍历 ideaA
        for (i = 0; i < n; ++i)
        {
            to = ideas[i][0] - 'a';
            for (j = 0; j < 26; ++j)
            {
                // 若 ideaA 的首字母由 to + 'a' 变为 j + 'a' 后不存在于 ideas 中，则 ideas 中所有将首字母由 j + 'a'变为 to + 'a' 后不存在于 ideas 中的字符串即为有效的 ideaB，其个数为 cnts[j][to]
                if(flags[i][j])
                    rst += cnts[j][to];
            }
        }

        return rst;
    }
};

时间复杂度为：O(c×n)O(c \times n) ；空间复杂度为：O(c×n)O(c \times n) 。其中 c 表示字母的种类数，为 26，n 表示 ideas 的长度。