本次周赛依旧只写出前三题，第四题到饭点了。（在家里，不吃饭要被线下gank）。

战局详情

排名用户名得分完成时间题目1（3）题目2（4）题目3（5）题目4（6）
844 / 6228Juruoer121:07:070:10:160:27:01 11:02:07

题目及解答

兼具大小写的最好英文字母

5242. 兼具大小写的最好英文字母

给你一个由英文字母组成的字符串 s ，请你找出并返回 s 中的 最好 英文字母。返回的字母必须为大写形式。如果不存在满足条件的字母，则返回一个空字符串。

最好 英文字母的大写和小写形式必须 都 在 s 中出现。

英文字母 b 比另一个英文字母 a 更好 的前提是：英文字母表中，b 在 a 之 后 出现。

提示：

  • 1 <= s.length <= 1000
  • s 由小写和大写英文字母组成

示例一：

输入：s = “lEeTcOdE”
输出：“E”
解释：
字母 ‘E’ 是唯一一个大写和小写形式都出现的字母。

示例二：

输入：s = “arRAzFif”
输出：“R”
解释：
字母 ‘R’ 是大写和小写形式都出现的最好英文字母。
注意 ‘A’ 和 ‘F’ 的大写和小写形式也都出现了，但是 ‘R’ 比 ‘F’ 和 ‘A’ 更好。

示例三：

输入：s = “AbCdEfGhIjK”
输出：“”
解释：
不存在大写和小写形式都出现的字母。

解决方案：

模拟：

按题意模拟即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution
{
public:
    string greatestLetter(string s)
    {
        char rst = ' ';
        char t;
        unordered_set<char> theSet; // 记录已经出现过的字母
        for(char c : s)
        {
            t = isupper(c) ? (c + 32) : (c - 32);
            
            if(theSet.count(t)) // 大小写都存在
                rst = max(rst, (isupper(c) ? c : t));
            
            theSet.emplace(c);
        }
        if(rst == ' ')
            return "";
        string r;
        r.push_back(rst);
        return r;
    }
};

时间复杂度：O(n)O(n) ；空间复杂度：O(c)O(c) 。其中 n 为 s 的长度，c 为字符的种类数，本题字符仅有26×2=5226 \times 2 = 52 种。

个位数字为 K 的整数之和

5218. 个位数字为 K 的整数之和

给你两个整数 num 和 k ，考虑具有以下属性的正整数多重集：

  • 每个整数个位数字都是 k 。
  • 所有整数之和是 num 。

返回该多重集的最小大小，如果不存在这样的多重集，返回 -1 。

注意：

  • 多重集与集合类似，但多重集可以包含多个同一整数，空多重集的和为 0 。
  • 个位数字 是数字最右边的数位。

提示：

  • 0 <= num <= 3000
  • 0 <= k <= 9

示例一：

输入：num = 58, k = 9
输出：2
解释：
多重集 [9,49] 满足题目条件，和为 58 且每个整数的个位数字是 9 。
另一个满足条件的多重集是 [19,39] 。
可以证明 2 是满足题目条件的多重集的最小长度。

示例二：

输入：num = 37, k = 2
输出：-1
解释：个位数字为 2 的整数无法相加得到 37 。

示例三：

输入：num = 0, k = 7
输出：0
解释：空多重集的和为 0 。

解决方案：

枚举：

由题意可知，若存在这样的多重集，则 num = (a1 * 10 + k) + (a2 * 10 + k) + ... + (an * 10 + k) = p * 10 + nk，n 即 该多重集的大小。

那么只需要枚举n，找到第一个满足 (num - n * k) % 10 == 0 的 n，即最小的多重集大小。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution
{
public:
    int minimumNumbers(int num, int k)
    {
        // 三个特判
        if (num == 0)
            return 0;
        if (k > num)
            return -1;
        if (k == 0)
            return (num % 10 == 0) ? 1 : -1;

        int n = 1;
        // 枚举 n
        while (num > 0)
        {
            num -= k;
            if (num % 10 == 0)
                return n;
            ++n;
        }
        // 不存在 n
        return -1;
    }
};

时间复杂度：O(num÷k)O(num \div k) ；空间复杂度：O(1)O(1) 。

小于等于 K 的最长二进制子序列

6099. 小于等于 K 的最长二进制子序列

给你一个二进制字符串 s 和一个正整数 k 。

请你返回 s 的 最长 子序列，且该子序列对应的 二进制 数字小于等于 k 。

注意：

  • 子序列可以有 前导 0 。
  • 空字符串视为 0 。
  • 子序列 是指从一个字符串中删除零个或者多个字符后，不改变顺序得到的剩余字符序列。

提示：

  • 1 <= s.length <= 1000
  • s[i] 要么是 '0' ，要么是 '1' 。
  • 1 <= k <= 1e9

示例一：

输入：s = “1001010”, k = 5
输出：5
解释：s 中小于等于 5 的最长子序列是 “00010” ，对应的十进制数字是 2 。
注意 “00100” 和 “00101” 也是可行的最长子序列，十进制分别对应 4 和 5 。
最长子序列的长度为 5 ，所以返回 5 。

示例二：

输入：s = “00101001”, k = 1
输出：6
解释：“000001” 是 s 中小于等于 1 的最长子序列，对应的十进制数字是 1 。
最长子序列的长度为 6 ，所以返回 6 。

解决方案：

一、贪心

从左到右遍历 s ，对于 s 的每一个字符，我们都将他放入二进制中，如果该二进制大于 k，由于 k >= 1 ，故 s 中一定存在 1，我们将第一个 1 从二进制中去除掉。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution
{
public:
    int longestSubsequence(string s, int k)
    {
        if(s == "")
            return 0;
        int rst = 0;
        int t;
        int num = 0; // 当前子字符串的十进制值
        int OneIdx = -1; // num 的二进制中第一个 1 的位置（自右往左）
        int _num;
        for(char c : s)
        {
            t = (num << 1) + c - '0';
            if(t > k) // 前面一定有 1，去除第一个 1，子字符串增加一位再去除一位，长度不变
            {
                num = ((num - (1 << OneIdx)) << 1) + c - '0';
                // 重新计算 OneIdx 的值
                if(num == 0)
                    OneIdx = -1;
                else
                {
                    _num = num;
                    OneIdx = -1;
                    while(_num)
                    {
                        _num >>= 1;
                        ++OneIdx;
                    }
                }
            }
            else // 子字符串长度加 1，第一个 1 的位置加 1
            {
                ++rst;
                num = t;
                if(num != 0)
                    ++OneIdx;
            }
        }
        return rst;
    }
};

时间复杂度：O(n×m)O(n \times m) ；空间复杂度：O(1)O(1)。其中 m 为 k 的二进制长度（首位为 1），n 为 s 的长度。

二、贪心 + 分类讨论

我们仔细观察方法一，发现方法一得出的子字符串一定包含 s 中的所有 0，所以只需要从 s 中找到二进制小于等于 k 的最长后缀，该后缀的长度加上 s 中除去该后缀的部分的所有 0 的个数即所求。

另外我们发现这个最长后缀若长度大于 k 的二进制的长度，则多出的高位必然为前导 0，所以我们只需要比较 s 的和 k 的二进制长度相同的后缀与 k 的关系即可。

设 s 的长度为 n，k 的二进制（首位为 1）的长度为 m。

  • 若 n <= m ，则 s 的所有后缀的二进制均小于等于 k，返回 n。
  • 若 n > m，且 s 的长为 m 的后缀的二进制小于等于 k，返回 s 中除去长为 m 的后的部分的 0 的个数 + m 。
  • 若 n > m，且 s 的成为 m 的后缀的二进制大于 k，说明 s 的长为 m 的后缀以 '1' 开头，又 s 的长为 m - 1 的后缀的二进制必小于 k，故返回 s 中除去长为 m 的后的部分的 0 的个数 + m - 1。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution
{
public:
    int longestSubsequence(string s, int k)
    {
        int n = s.size();
        int m = 0;
        int _k = k;
        
        // 计算 k 的二进制长度
        while(_k)
        {
            _k >>= 1;
            ++m;
        }
        
        if(n <= m)
            return n;
        
        // s 的长度为 m 的后缀为 s[n - m] ~ s[n - 1]
        int zCont = count(s.begin(), s.begin() + (n - m), '0'); // s 除去长度为 m 的后缀的部分的 0 的个数

        if(s[n - m] != '1') // 该后缀的二进制必然小于 k
            return zCont + m;

        int i, num = 0;
        for (i = n - m; i < n; ++i)
            num = (num << 1) + s[i] - '0';

        return num > k ? (zCont + m - 1) : (zCont + m);
    }
};

时间复杂度：O(n+m)O(n + m) ；空间复杂度：O(1)O(1) 。其中 m 为 k 的二进制长度（首位为 1），n 为 s 的长度。

卖木头块

5254. 卖木头块

给你两个整数 m 和 n ，分别表示一块矩形木块的高和宽。同时给你一个二维整数数组 prices ，其中 prices[i] = [hi, wi, pricei] 表示你可以以 pricei 元的价格卖一块高为 hi 宽为 wi 的矩形木块。

每一次操作中，你必须按下述方式之一执行切割操作，以得到两块更小的矩形木块：

  • 沿垂直方向按高度 完全 切割木块，或
  • 沿水平方向按宽度 完全 切割木块

在将一块木块切成若干小木块后，你可以根据 prices 卖木块。你可以卖多块同样尺寸的木块。你不需要将所有小木块都卖出去。你 不能 旋转切好后木块的高和宽。

请你返回切割一块大小为 m x n 的木块后，能得到的 最多 钱数。

注意你可以切割木块任意次。

提示：

  • 1 <= m, n <= 200
  • 1 <= prices.length <= 2 * 1e4
  • prices[i].length == 3
  • 1 <= hi <= m
  • 1 <= wi <= n
  • 1 <= pricei <= 1e6
  • 所有 (hi, wi) 互不相同 。

示例一：

示例一图

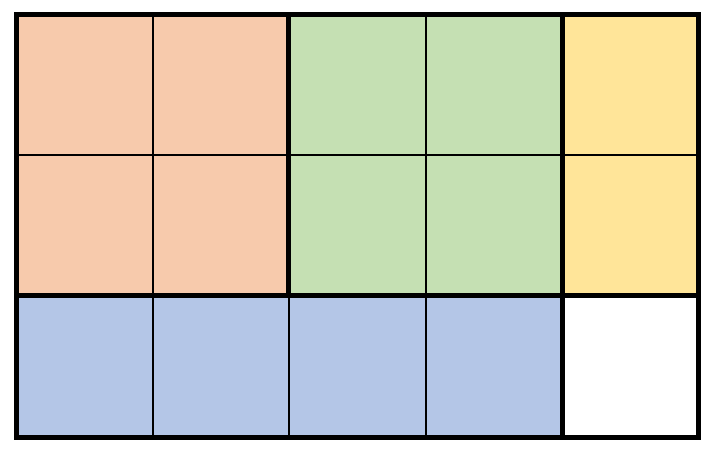
输入：m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
输出：19
解释：上图展示了一个可行的方案。包括：

  • 2 块 2 x 2 的小木块，售出 2 * 7 = 14 元。
  • 1 块 2 x 1 的小木块，售出 1 * 3 = 3 元。
  • 1 块 1 x 4 的小木块，售出 1 * 2 = 2 元。

总共售出 14 + 3 + 2 = 19 元。
19 元是最多能得到的钱数。

示例二：

示例二图

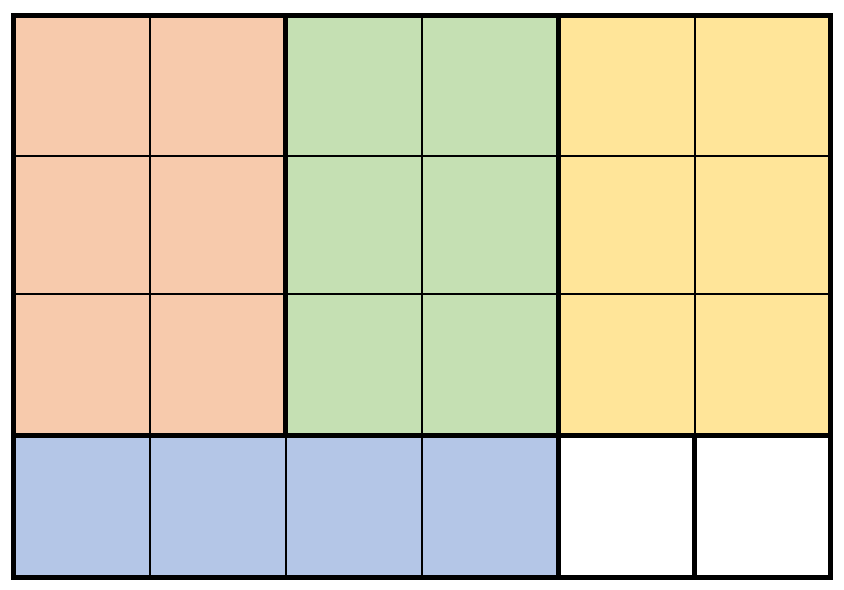
输入：m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
输出：32
解释：上图展示了一个可行的方案。包括：

  • 3 块 3 x 2 的小木块，售出 3 * 10 = 30 元。
  • 1 块 1 x 4 的小木块，售出 1 * 2 = 2 元。

总共售出 30 + 2 = 32 元。
32 元是最多能得到的钱数。
注意我们不能旋转 1 x 4 的木块来得到 4 x 1 的木块。

解决方案：

动态规划：

对于高度为 i 宽度为 j 的木块，假设其最多能卖出的价格为 dp[i][j]，我们可以将其分割为

  • 高度为 i ，宽度分别为 k 和 j - k 的两块，其中 k 大于 0 且 小于 j，或是
  • 宽度为 j ， 高度分别为 k 和 i - k 的两块，其中 k 大于 0 且 小于 i。

故 dp[i][j] = max(max(dp[i][k] + dp[i][j - k]), max(dp[k][j] + dp[i - k][j]))。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution
{
public:
    long long sellingWood(int m, int n, vector<vector<int>> &prices)
    {
        long long dp[m + 1][n + 1];
        memset(dp, 0, sizeof(dp));

        // 基础状态
        for(auto x : prices)
            dp[x[0]][x[1]] = x[2];

        int i, j, k;
        for (i = 1; i <= m; ++i)
        {
            for (j = 1; j <= n; ++j)
            {
                // 计算 高度为 i 宽度为 j 的木块发最佳分割方法
                for (k = 1; k < j; ++k) // 分割成 高度为 i 宽度分别为 k 和 j - k 的两块
                    dp[i][j] = max(dp[i][j], dp[i][k] + dp[i][j - k]);

                for (k = 1; k < i; ++k) // 分割成 宽度为 j 高度分别为 k 和 i - k 的两块
                    dp[i][j] = max(dp[i][j], dp[k][j] + dp[i - k][j]);
            }
        }

        return dp[m][n];
    }
};

时间复杂度：O(c+∑i=1m(i+∑j=1nj))=O(c+m×n×(2+m+n)2)=O(c+m×n×(m+n))O(c + \sum_{i = 1} ^ m(i + \sum_{j = 1} ^ n j)) = O(c + \frac{m \times n \times (2 + m + n)} {2}) = O(c + m \times n \times(m + n)) ；空间复杂度：O(m×n)O(m \times n)。其中 c 为 prices 的长度。