本次周赛依旧只写出前三题，第四题只想到时间复杂度为O(n2)O(n^2) 的方法。最可惜的是第三题，很简单的题目却花了很长时间。

战局详情

排名用户名得分完成时间题目1（3）题目2（4）题目3（5）题目4（6）
1895 / 6640Juruoer121:04:410:02:340:10:050:54:41 2

题目及解答

字母在字符串中的百分比

6074. 字母在字符串中的百分比

给你一个字符串 s 和一个字符 letter ，返回在 s 中等于 letter 字符所占的 百分比 ，向下取整到最接近的百分比。

提示：

  • 1 <= s.length <= 100
  • s 由小写英文字母组成
  • letter 是一个小写英文字母

示例一：

输入：s = “foobar”, letter = “o”
输出：33
解释：
等于字母 ‘o’ 的字符在 s 中占到的百分比是 2 / 6 * 100% = 33% ，向下取整，所以返回 33 。

示例二：

输入：s = “jjjj”, letter = “k”
输出：0
解释：
等于字母 ‘k’ 的字符在 s 中占到的百分比是 0% ，所以返回 0 。

解决方案：

统计出字符 letter 的个数即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution
{
public:
    int percentageLetter(string s, char letter)
    {
        int cnt = 0;
        for(char c : s)
            if(c == letter)
                ++cnt;
        return cnt * 100 / s.length();
    }
};

时间复杂度：O(n)O(n)，空间复杂度：O(1)O(1)，其中 n 表示 s 的字符数。

装满石头的背包的最大数量

6075. 装满石头的背包的最大数量

现有编号从 0 到 n - 1 的 n 个背包。给你两个下标从 0 开始的整数数组 capacity 和 rocks 。第 i 个背包最大可以装 capacity[i] 块石头，当前已经装了 rocks[i] 块石头。另给你一个整数 additionalRocks ，表示你可以放置的额外石头数量，石头可以往 任意 背包中放置。

请你将额外的石头放入一些背包中，并返回放置后装满石头的背包的 最大 数量。

提示：

  • n == capacity.length == rocks.length
  • 1 <= n <= 5 * 1e4
  • 1 <= capacity[i] <= 1e9
  • 0 <= rocks[i] <= capacity[i]
  • 1 <= additionalRocks <= 1e9

示例一：

输入：capacity = [2,3,4,5], rocks = [1,2,4,4], additionalRocks = 2
输出：3
解释：
1 块石头放入背包 0 ，1 块石头放入背包 1 。
每个背包中的石头总数是 [2,3,4,4] 。
背包 0 、背包 1 和 背包 2 都装满石头。
总计 3 个背包装满石头，所以返回 3 。
可以证明不存在超过 3 个背包装满石头的情况。
注意，可能存在其他放置石头的方案同样能够得到 3 这个结果。

示例二：

输入：capacity = [10,2,2], rocks = [2,2,0], additionalRocks = 100
输出：3
解释：
8 块石头放入背包 0 ，2 块石头放入背包 2 。
每个背包中的石头总数是 [10,2,2] 。
背包 0 、背包 1 和背包 2 都装满石头。
总计 3 个背包装满石头，所以返回 3 。
可以证明不存在超过 3 个背包装满石头的情况。
注意，不必用完所有的额外石头。

解决方案：

先统计出每个背包还需要多少块石头才能将背包装满，当额外的石头还足够时，优先装满需要石头数少的背包。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution
{
public:
    int maximumBags(vector<int> &capacity, vector<int> &rocks, int additionalRocks)
    {
        int i, n = capacity.size();
        vector<int> needs(n);
        for (i = 0; i < n; ++i)
            needs[i] = capacity[i] - rocks[i];
        
        sort(needs.begin(), needs.end());
        int rst = 0;
        for(i = 0; i < n; ++i)
        {
            if(additionalRocks >= needs[i])
            {
                ++rst;
                additionalRocks -= needs[i];
            }
            else
                return rst;
        }
        return rst;
    }
};

时间复杂度：O(nlog⁡(n))O(n\log(n))，空间复杂度：O(n)O(n)，其中 n 表示数组 capacity 的长度。也可以不需要 need 数组，重复利用 capacity 数组或 rocks 数组来代替 need，此时空间复杂度降为：O(1)O(1)。

表示一个折线图的最少线段数

6076. 表示一个折线图的最少线段数

给你一个二维整数数组 stockPrices ，其中 stockPrices[i] = [dayi, pricei] 表示股票在 dayi 的价格为 pricei 。折线图 是一个二维平面上的若干个点组成的图，横坐标表示日期，纵坐标表示价格，折线图由相邻的点连接而成。比方说下图是一个例子：

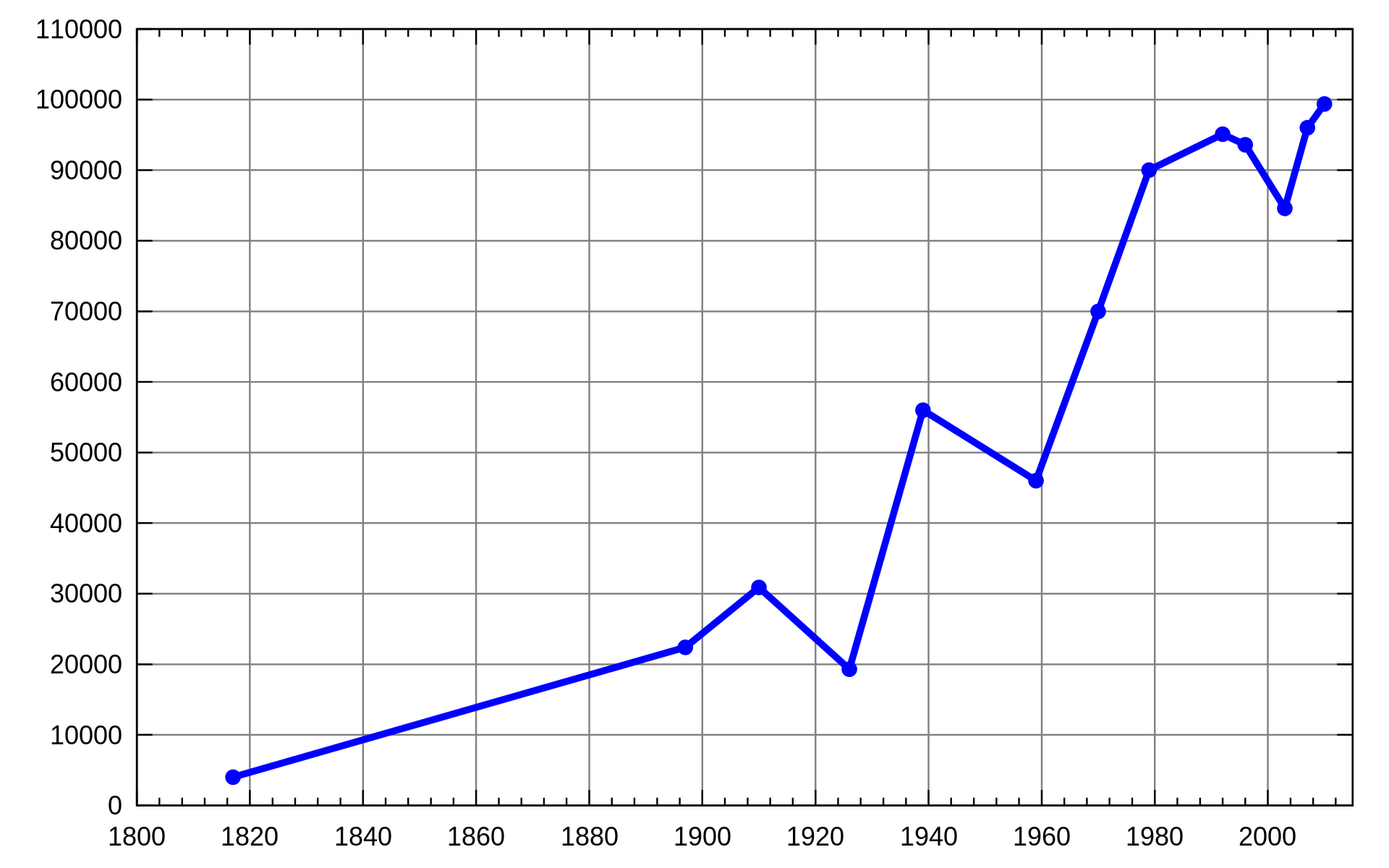
折线图示例

请你返回要表示一个折线图所需要的 最少线段数 。

提示：

  • 1 <= stockPrices.length <= 1e5
  • stockPrices[i].length == 2
  • 1 <= dayi, pricei <= 1e9
  • 所有 dayi 互不相同 。

示例一：

示例 1 图

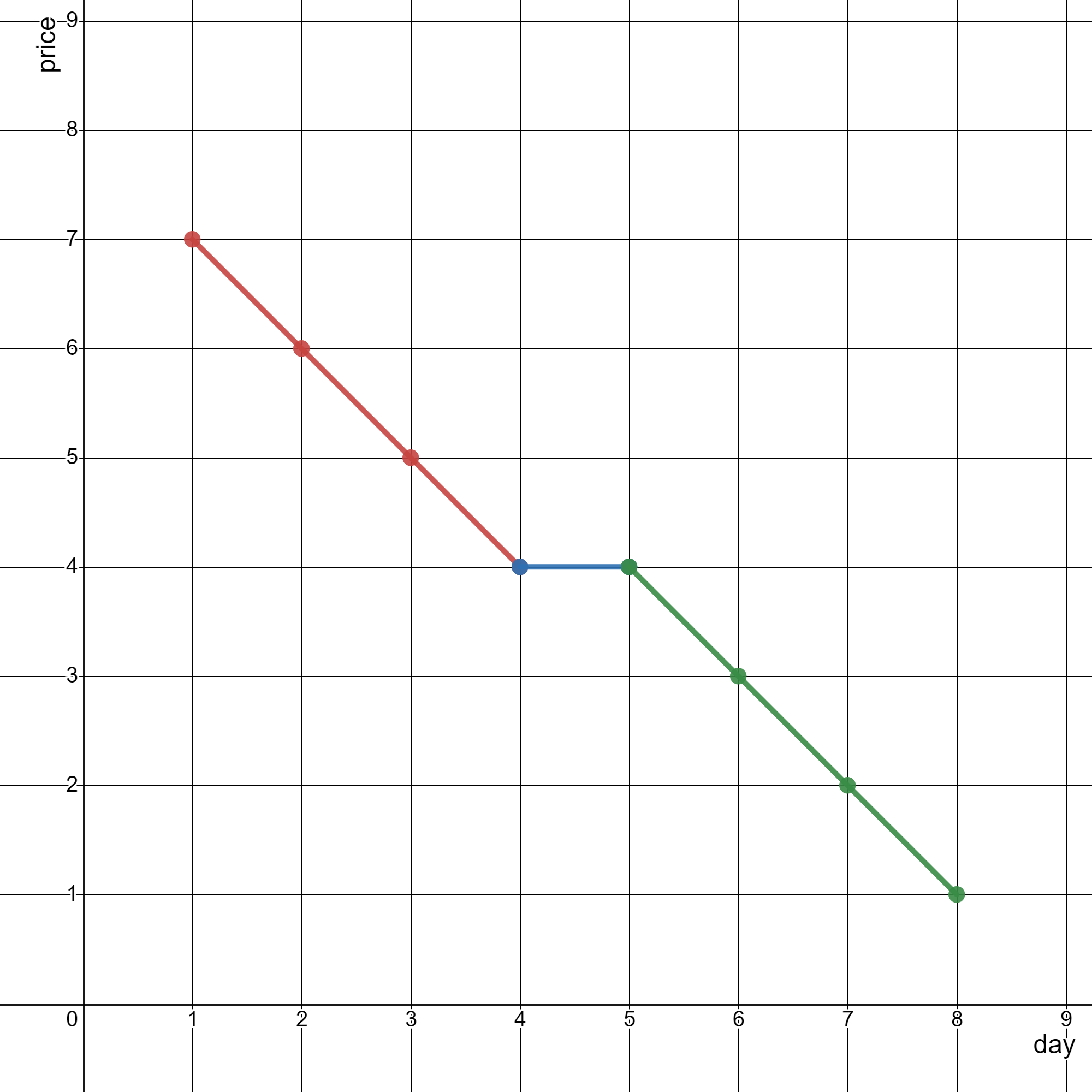
输入：stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
输出：3
解释：
上图为输入对应的图，横坐标表示日期，纵坐标表示价格。
以下 3 个线段可以表示折线图：

  • 线段 1 （红色）从 (1,7) 到 (4,4) ，经过 (1,7) ，(2,6) ，(3,5) 和 (4,4) 。
  • 线段 2 （蓝色）从 (4,4) 到 (5,4) 。
  • 线段 3 （绿色）从 (5,4) 到 (8,1) ，经过 (5,4) ，(6,3) ，(7,2) 和 (8,1) 。

可以证明，无法用少于 3 条线段表示这个折线图。

示例二：

示例 2 图

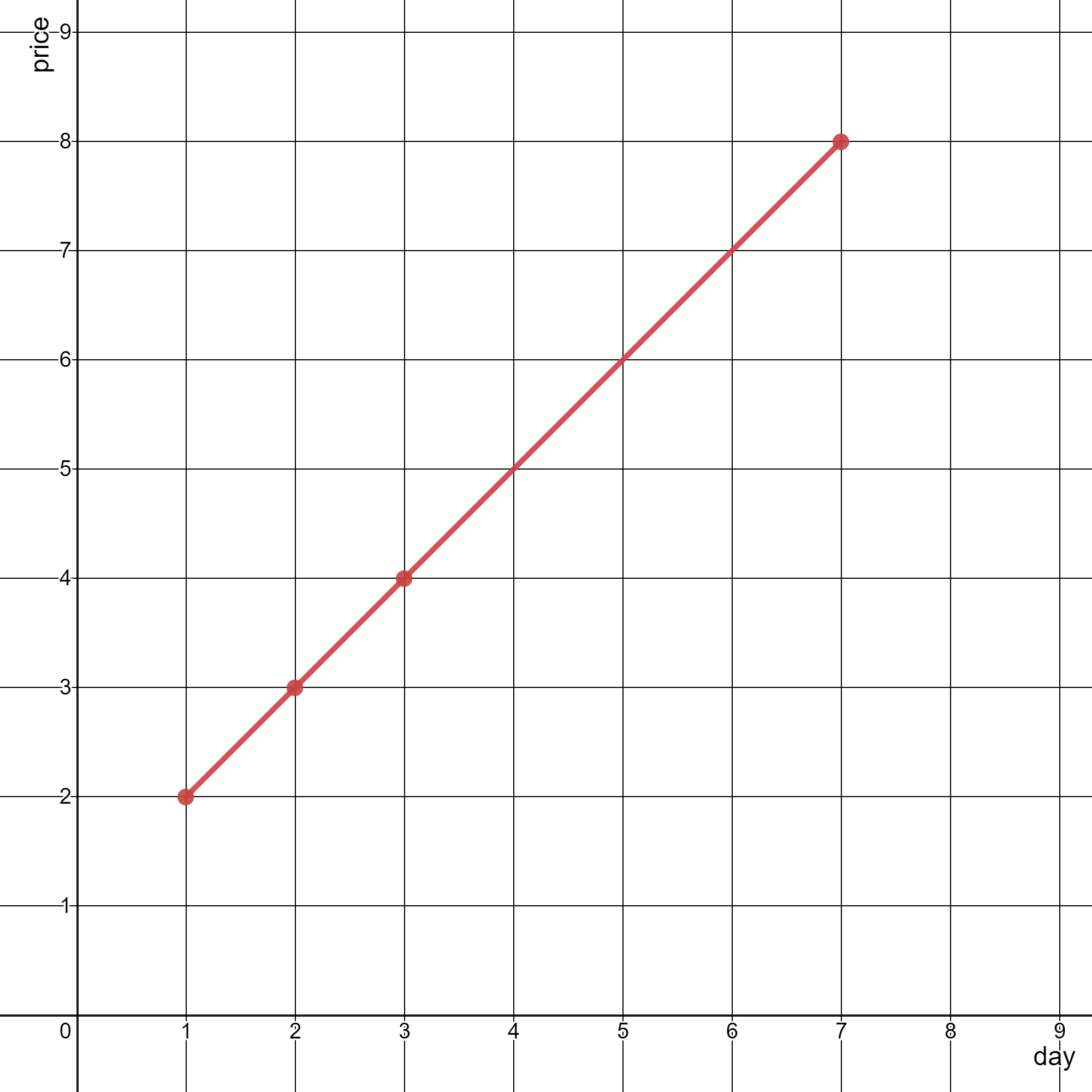
输入：stockPrices = [[3,4],[1,2],[7,8],[2,3]]
输出：1
解释：
如上图所示，折线图可以用一条线段表示。

解决方案：

先将所有点按 x 轴从左到右排序（即按照日期从小到大排序），然后从第三个点开始计算该点与该点左边的两个点是否共线，若共线则该点与前两点在同一线段上，否则该点与左边的一个点形成一条新的线段。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution
{
public:
    int minimumLines(vector<vector<int>> &stockPrices)
    {
        int n = stockPrices.size();
        if(n == 1) // 自有一个点，无法形成线段
            return 0;
        // 将所有点按 x 轴从左到右排序（即按照日期从小到大排序）
        sort(stockPrices.begin(), stockPrices.end(), [](const vector<int> &a, const vector<int> &b)
             { return a[0] < b[0]; });
        
        int cnt = 1; // 第一个点与第二个点形成的线段
        
        // 从第三个点开始计算是否有新的线段
        for (int i = 2; i < n; ++i)
        {
            // 设 stockPrices[i - 2] 为点 p(px, py)，stockPrices[i - 1] 为点 q(qx, qy)，stockPrices[i] 为点 r(rx, ry)
            // p、q、r 共线即 pq、qr 斜率相等，即：
            // (Δy / Δx == Δ_y / Δ_x) ==> (Δy * Δ_x == Δ_y * Δx)
            // 其中 Δx = rx - qx, Δy = ry - qy, Δ_x = qx - px, Δ_y = qy - py
            if(1LL * (stockPrices[i][1] - stockPrices[i - 1][1]) * (stockPrices[i - 1][0] - stockPrices[i - 2][0]) != 1LL * (stockPrices[i - 1][1] - stockPrices[i - 2][1]) * (stockPrices[i][0] - stockPrices[i - 1][0]))
                ++cnt;
        }
        return cnt;
    }
};

时间复杂度：O(nlog⁡(n))O(n\log(n))，空间复杂度为O(1)O(1)，其中 n 表示数组 stockPrices 的长度。

巫师的总力量和

6077. 巫师的总力量和

作为国王的统治者，你有一支巫师军队听你指挥。

给你一个下标从 0 开始的整数数组 strength ，其中 strength[i] 表示第 i 位巫师的力量值。对于连续的一组巫师（也就是这些巫师的力量值是 strength 的 子数组），总力量 定义为以下两个值的 乘积 ：

  • 巫师中 最弱 的能力值。
  • 组中所有巫师的个人力量值 之和 。

请你返回 所有 巫师组的 总 力量之和。由于答案可能很大，请将答案对 1e9 + 7 取余 后返回。

子数组 是一个数组里 非空 连续子序列。

提示：

  • 1 <= strength.length <= 1e5
  • 1 <= strength[i] <= 1e9

示例一：

输入：strength = [1,3,1,2]
输出：44
解释：以下是所有连续巫师组：

  • [1,3,1,2] 中 [1] ，总力量值为 min([1]) * sum([1]) = 1 * 1 = 1
  • [1,3,1,2] 中 [3] ，总力量值为 min([3]) * sum([3]) = 3 * 3 = 9
  • [1,3,1,2] 中 [1] ，总力量值为 min([1]) * sum([1]) = 1 * 1 = 1
  • [1,3,1,2] 中 [2] ，总力量值为 min([2]) * sum([2]) = 2 * 2 = 4
  • [1,3,1,2] 中 [1,3] ，总力量值为 min([1,3]) * sum([1,3]) = 1 * 4 = 4
  • [1,3,1,2] 中 [3,1] ，总力量值为 min([3,1]) * sum([3,1]) = 1 * 4 = 4
  • [1,3,1,2] 中 [1,2] ，总力量值为 min([1,2]) * sum([1,2]) = 1 * 3 = 3
  • [1,3,1,2] 中 [1,3,1] ，总力量值为 min([1,3,1]) * sum([1,3,1]) = 1 * 5 = 5
  • [1,3,1,2] 中 [3,1,2] ，总力量值为 min([3,1,2]) * sum([3,1,2]) = 1 * 6 = 6
  • [1,3,1,2] 中 [1,3,1,2] ，总力量值为 min([1,3,1,2]) * sum([1,3,1,2]) = 1 * 7 = 7

所有力量值之和为 1 + 9 + 1 + 4 + 4 + 4 + 3 + 5 + 6 + 7 = 44 。

示例二：

输入：strength = [5,4,6]
输出：213
解释：以下是所有连续巫师组：

  • [5,4,6] 中 [5] ，总力量值为 min([5]) * sum([5]) = 5 * 5 = 25
  • [5,4,6] 中 [4] ，总力量值为 min([4]) * sum([4]) = 4 * 4 = 16
  • [5,4,6] 中 [6] ，总力量值为 min([6]) * sum([6]) = 6 * 6 = 36
  • [5,4,6] 中 [5,4] ，总力量值为 min([5,4]) * sum([5,4]) = 4 * 9 = 36
  • [5,4,6] 中 [4,6] ，总力量值为 min([4,6]) * sum([4,6]) = 4 * 10 = 40
  • [5,4,6] 中 [5,4,6] ，总力量值为 min([5,4,6]) * sum([5,4,6]) = 4 * 15 = 60

所有力量值之和为 25 + 16 + 36 + 36 + 40 + 60 = 213 。

解决方案：

一、暴力穷举

设数组 strength 的长度为 n，则该数组共有∑i=1nn−i+1=n2+n2\sum_{i=1}^n n - i + 1 = \frac{n^2 + n}{2} 个子序列（长度为 i 的子序列有 n - i + 1 个），对每个子序列求和及最小值需要遍历该子序列，则时间复杂度为：

O(∑i=1n(i⋅(n−i+1)))=O(n3+3n2+2n6)=O(n3)O \bigg ( \sum_{i=1}^n \big (i \cdot (n - i + 1) \big ) \bigg ) = O \big ( \frac{n^3 + 3n^2 + 2n}6 \big ) = O(n^3)

显然时间复杂度过高，必然 TLE。

优化方法：假设我们已经计算出了长度为 s 的所有子序列的和及最小值，则计算长度为 s + 1 的子数组的和及最小值时不需要重新遍历这些子序列，可以由之前的结果来推导。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution
{
public:
    int totalStrength(vector<int> &strength)
    {
        int i, n = strength.size();
        int rst = 0;
        int p = 1e9 + 7;
        vector<pair<long long, int>> dp(n); // 由于存储各子序列的长度和最小值
        // 计算长度为 1 的所有子序列的和及最小值并存储在 dp 中
        for (i = 0; i < strength.size(); ++i)
        {
            dp[i] = make_pair(strength[i], strength[i]);
            rst = (rst + dp[i].first * dp[i].second) % p;
        }
        // 利用 dp 计算长度为 s 的所有子序列的和及最小值并存储在 dp[s - 1] ~ dp[n - 1] 中
        for (int s = 2; s <= n; ++s)
        {
            // 长度为 s 的子序列 sub 的和即 以相同的下标（设为 i）结束的 长度为 s - 1 的子序列 _sub 的和 加上 strength[i - s + 1]，而最小值即 _sub 的最小值和 streng[i - s + 1] 的最小值。
            for (i = s - 1; i < n; ++i)
            {
                dp[i].first += strength[i + 1 - s];
                dp[i].second = min(dp[i].second, strength[i + 1 - s]);
                rst = (rst + dp[i].first * dp[i].second) % p;
            }
        }
        return rst;
    }
};

时间复杂度降低为：O(n2)O(n ^ 2)，但仍然 TLE。

二、单调栈 + 前缀和

参照 灵茶山艾府 大佬的 题解。

本题与 LeetCode 上的 907. 子数组的最小值之和 类似，可以先求出以数组中某个元素 strength[i] 为 最小值 的所有子序列的下标范围 [left, right]，即在 strength[left ~ right] 范围内所有含有 strength[i]（值相同不行，必须是下标为 i）的子序列的最小值均为 strength[i]。为了避免 strength[i] = strength[j] 而导致的范围的重叠，定义当 i > left 时，strength[left ~ i - 1] 的所有值 严格小于 strength[i]；当 i < right 时，strength[i + 1 ~ right] 的所有值 小于等于 strength[i]。

该范围的简单的计算方法是：对于 strength[i]，找到其左边最后一个大于等于它的值的下标 l，则 left = l + 1；再找到其右边第一个大于它的值的下标 r，则 right = r - 1，但此时间复杂度为O(n2)O(n ^ 2)

可以使用一个单调递增栈 st 优化计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 计算以 strength[i] 为最小值的子序列的区间 [left, right]
int i, n = strength.size();
stack<int> st;
vector<int> left(n); // 以 strength[i] 为最小值的子序列的最左边界
vector<int> right(n, n - 1); // 以 strength[i] 为最小值的子序列的最右边界
st.push(-1);
for (i = 0; i < n; ++i)
{
    while (st.top() != -1 && strength[i] < strength[st.top()])
    {
        right[st.top()] = i - 1;
        st.pop();
    }
    
    left[i] = st.top() + 1;
    st.push(i);
}

因为每一个元素只入栈和出栈一次，时间复杂度为O(n)O(n)。

对于 strength[i] ，其对最终结果产生的贡献为：strength[i] 乘以 strength[left[i] ~ right[i]] 范围内所有含有 strength[i]（必须是该下标值） 的子序列的和的和。

设 strength 的前缀和为 sum，其中sum[i]=∑j=0i−1strength[i]sum[i] = \sum_{j=0}^{i-1} strength[i]，故子数组 [l, r] 的元素和为 sum[r + 1] - sum[l]。

设 sum 的前缀和为 ssum，其中ssum[i]=∑j=0i−1sum[i]ssum[i] = \sum_{j=0}^{i-1}sum[i]，故 sum[L ~ R] 的和为 ssum[R + 1] - ssum[L]。

则 strength[left[i] ~ right[i]] （方便期间，令 L = left[i]，R = right[i]）范围内所有含有 strength[i]（必须是该下标值） 的子序列的和的和可以表示为：

∑l=Li∑r=i+1R+1(sum[r]−sum[l])=∑l=Li(∑r=i+1R+1sum[r]−(R−i+1)⋅sum[l])=(i−L+1)⋅∑r=i+1R+1sum[r]−(R−i+1)⋅∑l=left[i]isum[l]=(i−L+1)⋅(ssum[R+2]−ssum[i+1])−(R−i+1)⋅(ssum[i+1]−ssum[L])\begin{align} \sum_{l=L}^{i} \sum_{r=i+1}^{R+1}(sum[r]-sum[l]) &= \sum_{l=L}^{i} \bigg ( \sum_{r=i+1}^{R+1}sum[r] - (R - i + 1) \cdot sum[l] \bigg )\\ &= (i - L + 1) \cdot \sum_{r=i+1}^{R+1}sum[r] - (R - i + 1) \cdot \sum_{l=left[i]}^{i}sum[l]\\ &= (i - L + 1) \cdot (ssum[R+2] - ssum[i+1]) - (R - i + 1) \cdot (ssum[i+1] - ssum[L]) \end{align}

计算出所有元素的贡献并累加即为答案。

最终代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution
{
public:
    int totalStrength(vector<int> &strength)
    {
        int i, n = strength.size();
        int rst = 0;
        int p = 1e9 + 7;

        long long sum = 0L; // strength的前缀和
        vector<int> ssum(n + 2); // strength 的前缀和的前缀和
        for (i = 1; i <= n; ++i)
        {
            sum += strength[i - 1];
            ssum[i + 1] = (ssum[i] + sum) % p;
        }

        // 计算以 strength[i] 为最小值的子序列的区间 [left, right]
        stack<int> st;
        vector<int> left(n); // 以 strength[i] 为最小值的子序列的最左边界
        vector<int> right(n, n - 1); // 以 strength[i] 为最小值的子序列的最右边界
        st.push(-1);
        for (i = 0; i < n; ++i)
        {
            while (st.top() != -1 && strength[i] < strength[st.top()])
            {
                right[st.top()] = i - 1;
                st.pop();
            }
            
            left[i] = st.top() + 1;
            st.push(i);
        }

        // 计算 streng[i] 对结果的贡献，并求和
        for (i = 0; i < n; ++i)
        {
            long long t = (1LL * (i - left[i] + 1) * (ssum[right[i] + 2] - ssum[i + 1]) - 1LL * (right[i] - i + 1) * (ssum[i + 1] - ssum[left[i]])) % p;
            rst = (rst + strength[i] * t) % p;
        }
        // 防止 rst 为负数（t 的计算含有减号）
        return (rst + p) % p;
    }
};

时间复杂度为：O(n)O(n)，空间复杂度为O(n)O(n)。