记录 LeetCode 第 295 场周赛

本次周赛惨遭滑铁卢，仅仅写出第一题。前一天睡的太晚了，比赛的时候浑浑噩噩。第二题由于 double 强转 int 的精度问题，一直 WA，第三题又没有什么思路，第四题压根没看 ~~（可惜第四题直接 Dijkstra 就可以 AC）~~ 。

战局详情

排名	用户名	得分	完成时间	题目1（3）	题目2（4）	题目3（5）	题目4（6）
3944 / 6640	Juruoer	3	0:08:13

题目及解答

重排字符形成目标字符串

2287. 重排字符形成目标字符串

给你两个下标从 0 开始的字符串 s 和 target 。你可以从 s 取出一些字符并将其重排，得到若干新的字符串。

从 s 中取出字符并重新排列，返回可以形成 target 的最大副本数。

提示：

1 <= s.length <= 100
1 <= target.length <= 10
s 和 target 由小写英文字母组成

示例一：

输入：s = “ilovecodingonleetcode”, target = “code”
输出：2
解释：
对于 “code” 的第 1 个副本，选取下标为 4 、5 、6 和 7 的字符。
对于 “code” 的第 2 个副本，选取下标为 17 、18 、19 和 20 的字符。
形成的字符串分别是 “ecod” 和 “code” ，都可以重排为 “code” 。
可以形成最多 2 个 “code” 的副本，所以返回 2 。

示例二：

输入：s = “abcba”, target = “abc”
输出：1
解释：
选取下标为 0 、1 和 2 的字符，可以形成 “abc” 的 1 个副本。
可以形成最多 1 个 “abc” 的副本，所以返回 1 。
注意，尽管下标 3 和 4 分别有额外的 ‘a’ 和 ‘b’ ，但不能重用下标 2 处的 ‘c’ ，所以无法形成 “abc” 的第 2 个副本。

示例三：

输入：s = “abbaccaddaeea”, target = “aaaaa”
输出：1
解释：
选取下标为 0 、3 、6 、9 和 12 的字符，可以形成 “aaaaa” 的 1 个副本。
可以形成最多 1 个 “aaaaa” 的副本，所以返回 1 。

解决方案：

计算 s 中每个字符的个数分别为 target 中每个字符的个数的多少倍，取最小倍数即为答案。

代码：

class Solution
{
public:
    int rearrangeCharacters(string s, string target)
    {
        vector<int> cnts(26, 0);
        vector<int> have(26, 0);
        int rst = 0x7fffffff;
        for(char c : target)
        {
            ++cnts[c - 'a'];
        }
        for (char c : s)
        {
            ++have[c - 'a'];
        }
        for (int i = 0; i < 26; ++i)
        {
            if(cnts[i] > 0)
                rst = min(rst, have[i] / cnts[i]);
        }
        return rst;
    }
};

时间复杂度为： $O(m + n)$ ，空间复杂度为： $O(m + n)$ ，m 和 n 分别为 s 和 target 的长度。

价格减免

2288. 价格减免

句子是由若干个单词组成的字符串，单词之间用单个空格分隔，其中每个单词可以包含数字、小写字母、和美元符号 '$' 。如果单词的形式为美元符号后跟着一个非负实数，那么这个单词就表示一个价格。

例如 "$100"、"$23" 和 "$6.75" 表示价格，而 "100"、"$" 和 "2$3" 不是。

注意：本题输入中的价格均为整数。

给你一个字符串 sentence 和一个整数 discount 。对于每个表示价格的单词，都在价格的基础上减免 discount% ，并更新该单词到句子中。所有更新后的价格应该表示为一个 恰好保留小数点后两位 的数字。

返回表示修改后句子的字符串。

提示：

1 <= sentence.length <= 1e5
sentence 由小写英文字母、数字、' ' 和 '$' 组成
sentence 不含前导和尾随空格
sentence 的所有单词都用单个空格分隔
所有价格都是正整数且不含前导零
所有价格最多为 10 位数字
0 <= discount <= 100

示例一：

输入：sentence = “there are $1 $2 and 5$ candies in the shop”, discount = 50
输出：“there are $0.50 $1.00 and 5$ candies in the shop”
解释：
表示价格的单词是 “$1” 和 “$2” 。

“$1” 减免 50% 为 “$0.50” ，所以 “$1” 替换为 “$0.50” 。
“$2” 减免 50% 为 “$1” ，所以 “$1” 替换为 “$1.00” 。

示例二：

输入：sentence = “1 2 $3 4 $5 $6 7 8$ $9 $10$”, discount = 100
输出：“1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$”
解释：
任何价格减免 100% 都会得到 0 。
表示价格的单词分别是 “$3”、“$5”、“$6” 和 “$9”。
每个单词都替换为 “$0.00”。

解决方案：

字符串模拟题，遍历字符串 sentence （也可以使用正则表达式），对于所有的价格计算出新的价格，构造新的字符串即可。

需要注意的是，此题要求保留两位小数，但若使用 float 类型或 double 类型强转成 int 类型会有精度错误，当然也可以不强转，而使用字符流 ostringstream 来格式化地将浮点型 保留指定小数位 并转为 ostringstream 型，再获取相应 string 型：

//对于浮点型价格 price 保留两位小数转为字符流
ostringstream oss;
oss << fixed << setprecision(2) << price;

oss.str();

也可以不使用浮点型，由于本题 discount 属于 0 到 100，故对于价格 price，price * (100 - discount) 即为打折后的价格的 100 倍，其最后两位数即为小数点后的值，且没有精度问题。

代码：

class Solution
{
public:
    string discountPrices(string sentence, int discount)
    {
        int i = 0, j = 0, k, n = sentence.length();
        int r = 100 - discount;
        long long num;
        bool isDig;
        string rst = "";
        string temp;
        while (i < n + 1)
        {
            if(i == n || sentence[i] == ' ') // 每有一个新的单词
            {
                temp = sentence.substr(j, i - j); // 取出该单词
                if (temp[0] != '$' || temp.size() > 11 || temp.size() < 2) // 该单词明显不是价格
                    rst.append(temp);
                else
                {
                    isDig = true;
                    num = 0;
                    for (k = 1; k < temp.size(); ++k)
                    {
                        if(!isdigit(temp[k])) // 该单词依旧不是价格
                        {
                            isDig = false;
                            rst.append(temp);
                            break;
                        }
                        num = num * 10 + temp[k] - '0';
                    }
                    if(isDig)
                    {
                        num *= r; // 计算出打折后的价格的100倍
                        rst.push_back('$');
                        rst.append(to_string(num / 100)); // 小数点前的数
                        num = num % 100; // 小数点后的数
                        rst.push_back('.');
                        if(num < 10) // 若后两位为 0x，则补充第一个0
                            rst.push_back('0');
                        rst.append(to_string(num));
                    }
                }
                j = i + 1;
                if(i != n)
                    rst.push_back(' ');
            }
            ++i;
        }
        return rst;
    }
};

时间复杂度： $O(n)$ ，空间复杂度： $O(n)$ ，n 为 sentence 的长度。

使数组按非递减顺序排列

2289. 使数组按非递减顺序排列

给你一个下标从 0 开始的整数数组 nums 。在一步操作中，移除所有满足 nums[i - 1] > nums[i] 的 nums[i] ，其中 0 < i < nums.length 。

重复执行步骤，直到 nums 变为 非递减 数组，返回所需执行的操作数。

提示：

1 <= nums.length <= 1e5
1 <= nums[i] <= 1e9

示例一：

输入：nums = [5,3,4,4,7,3,6,11,8,5,11]
输出：3
解释：执行下述几个步骤：

步骤 1 ：[5,3,4,4,7,3,6,11,8,5,11] 变为 [5,4,4,7,6,11,11]
步骤 2 ：[5,4,4,7,6,11,11] 变为 [5,4,7,11,11]
步骤 3 ：[5,4,7,11,11] 变为 [5,7,11,11]
[5,7,11,11] 是一个非递减数组，因此，返回 3 。

示例二：

输入：nums = [4,5,7,7,13]
输出：0
解释：nums 已经是一个非递减数组，因此，返回 0 。

解决方案：

若直接模拟，则时间复杂度为 $O(n^2)$ 显然 TLE。

可以使用单调栈 + 动态规划计算。

以下的 x 被 y 删除的意思是，经过一系列删除操作后 y 为 x 的前一个元素，且 y > x。

此段来自灵茶山艾府的题解的提示2：
nums[i] 若被删除，则一定是被 nums[i] 左边的某个值删除，可以证明， nums[i] 若被删除，则其被删除所需的步数可以等价于被其左边第一个大于 nums[i] 的值（设为 nums[j]）删除所需的步数。
以 [20,1,9,1,2,3] 为例。
时刻一 20 删掉 1，9 删掉 1；
时刻二 20 删掉 9，9 删掉 2;
时刻三 20 接替了 9 的任务，来删除数字 3。
虽然说数字 3 是被 20 删除的，但是由于 20 立马接替了 9，我们可以等价转换成 3 是被 9 删除的，也就是它左边离它最近且比它大的那个数。这一等价转换不会影响数字被删除的时刻。

可以使用单调递减栈来计算每个元素左边第一个大于其的元素。

设删除 nums[i] 所需的步数为 dp[i] (若 nums[i] 不需要删除，则 dp[i] 等于 0)，且假设 nums[i] 被 nums[j] 删除（或根据上述所说的等价于被nums[j]删除），则 nums[j + 1] 到 nums[i - 1] 均已被删除，则：

dp[i] = max(dp[j + 1], dp[j + 2], ... , dp[i - 1]) + 1。

单调递减栈出栈时刚好会将 nums[i] 左边小于其的值取出直至遇到 nums[j] 或栈空(即 nums[i] 无需删除)。

代码：

class Solution
{
public:
    int totalSteps(vector<int> &nums)
    {
        stack<int> st; // 单调递减栈
        int rst = 0, i, n = nums.size(), step;
        int dp[n];
        for (i = 0; i < n; ++i)
        {
            step = 0;
            // 找到左边第一个大于 nums[i] 的元素 nums[j]，并计算出 step = max(dp[j + 1], dp[j + 2], ... , dp[i - 1])
            while(st.size() && nums[i] >= nums[st.top()])
            {
                step = max(step, dp[st.top()]);
                st.pop();
            }
            if(st.size()) // 若栈中还有元素，说明 nums[i] 需要被删除，且删除步数为 step + 1
            {
                dp[i] = step + 1;
                rst = max(rst, dp[i]); // 更新最大值
            }
            else
                dp[i] = 0;

            st.push(i);
        }
        return rst;
    }
};

时间复杂度： $O(n)$ ，空间复杂度： $O(n)$ ，n 为 nums 的长度。

到达角落需要移除障碍物的最小数目

6081. 到达角落需要移除障碍物的最小数目

给你一个下标从 0 开始的二维整数数组 grid ，数组大小为 m x n 。每个单元格都是两个值之一：

0 表示一个空单元格，
1 表示一个可以移除的 障碍物 。

你可以向上、下、左、右移动，从一个空单元格移动到另一个空单元格。

现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1) ，返回需要移除的障碍物的最小数目。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 1e5
2 <= m * n <= 1e5
grid[i][j] 为 0 或 1
grid[0][0] == grid[m - 1][n - 1] == 0

示例一：

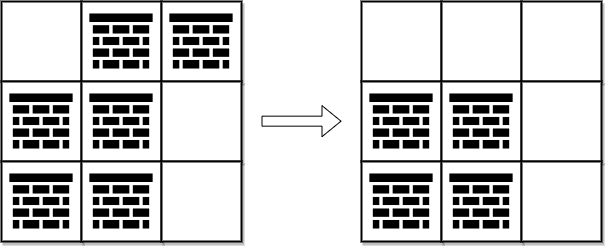
输入：grid = [[0,1,1],[1,1,0],[1,1,0]]
输出：2
解释：可以移除位于 (0, 1) 和 (0, 2) 的障碍物来创建从 (0, 0) 到 (2, 2) 的路径。
可以证明我们至少需要移除两个障碍物，所以返回 2 。
注意，可能存在其他方式来移除 2 个障碍物，创建出可行的路径。

示例二：

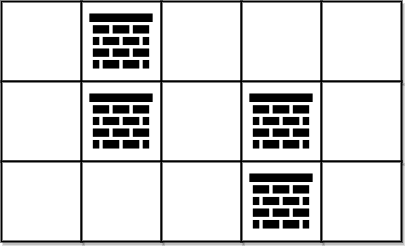
输入：grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
输出：0
解释：不移除任何障碍物就能从 (0, 0) 到 (2, 4) ，所以返回 0 。

解决方案：

单源最短路径问题，空格子表示路径花销为 0，障碍物表示路径花销为 1。

方法一、Dijkstra 算法

Dijkstra 算法是很有名的算法了，不作过多解释，这里使用一个小根堆来维护待计算的点。

代码：

class Solution {
public:
    typedef tuple<int, int, int> tiii;
    struct cmp
    {
        bool operator()(const tiii &a, const tiii &b)
        {
            return get<2>(a) > get<2>(b);
        }
    };

    int minimumObstacles(vector<vector<int>> &grid)
    {
        int m = grid.size();
        int n = grid[0].size();
        int cx, cy, nx, ny;
        int cdis;
        int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

        // 小根堆，将 “未访问过” 的点按距离从小到大排列（因为有环，故该点也可能访问过，但是后续会判断，且队列中不一定包含所有未访问点，但队头元素一定是未访问的点中距离(0, 0)点最近的点）
        // 对于所有 已访问过 的点，其最近距离已经计算完成了。
        priority_queue<tiii, vector<tiii>, cmp> qu;

        int dis[m][n]; // 距离数组
        bool vis[m][n]; // 访问标记

        memset(dis, 0x7f, sizeof(dis)); // 初始化所有距离为 0x7f7f7f7f，虽然不是 int 最大值，但大于 m + n

        memset(vis, false, sizeof(vis)); // 开始时未访问任何点

        // 初始化第一个点
        dis[0][0] = grid[0][0]; 
        qu.emplace(0, 0, dis[0][0]);

        while(qu.size()) // 还有 “未访问过” 的点
        {
            tie(cx, cy, cdis) = qu.top();
            qu.pop();
            if(vis[cx][cy]) // 若已经访问过，跳过
                continue;
            vis[cx][cy] = true; // 标记为已访问过

            for(auto &dir : dirs) // 遍历该点可以直接到达的点
            {
                nx = cx + dir[0];
                ny = cy + dir[1];
                if(nx < 0 || ny < 0 || nx >= m || ny >= n || vis[nx][ny]) // 点坐标不合法或已经访问过
                    continue;
                if(cdis + grid[nx][ny] < dis[nx][ny]) // 更新距离
                {
                    dis[nx][ny] = cdis + grid[nx][ny];
                    // 若未更新距离，说明有一条跟近的路线到达 点(nx, ny)，则点 (nx, ny) 要么已经访问过了，要么已经存在于 qu 中了
                    qu.emplace(nx, ny, dis[nx][ny]);
                }
            }
        }
        return dis[m - 1][n - 1];
    }
};

时间复杂度： $O(mnlog(mn))$ ，空间复杂度 $O(mn)$ ，m，n 分别表示 grid 的行数和列数。

方法二、0-1 BFS

bfs 可以解决所有路径花销为 1 的图的最短理解问题，而 0-1bfs 则可以解决所有路径花销为 0 或 1 的图的最短路径问题。

只要稍微修改 bfs 算法，使得每次计算时优先计算路径花销为 0 的节点，相当于花销为 0 的节点被 “无视掉”，即其前驱节点视为可以 “直接” 连到其后继节点，亦相当于减少花销为 0 的节点的后继结点 bfs 的的层数。

由于只有成功更新距离才会将点入队，但每个点第一次跟新距离后其实就已经计算出最短路径了（因为是层序遍历，虽然可能还有其他的路径可以到达该点，但是距离一定不会小于第一次计算出的距离），所以不需要访问标记 vis，也不会出现环。

代码：

class Solution
{
public:
    typedef pair<int, int> pii;
    int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    int minimumObstacles(vector<vector<int>> &grid)
    {
        int m = grid.size();
        int n = grid[0].size();
        int dis[m][n];
        int nx, ny, d;
        memset(dis, 0x7f, sizeof(dis));
        dis[0][0] = 0;
        deque<pii> dq; // 双端队列
        dq.emplace_front(0, 0);
        while(dq.size())
        {
            auto [cx, cy] = dq.front();
            dq.pop_front();
            for(auto &dir : dirs)
            {
                nx = cx + dir[0];
                ny = cy + dir[1];
                if(nx < 0 || ny < 0 || nx >= m || ny >= n)
                    continue;
                d = grid[nx][ny];
                if(dis[cx][cy] + d < dis[nx][ny]) // 更新距离
                {
                    dis[nx][ny] = dis[cx][cy] + d;
                    // 若花销为 0，则将其插入队头，否则插入队尾
                    d == 0 ? dq.emplace_front(nx, ny) : dq.emplace_back(nx, ny);
                }
            }
        }
        return dis[m - 1][n - 1];
    }
};

时间复杂度： $O(mn)$ ，空间复杂度 $O(mn)$ ，m，n 分别表示 grid 的行数和列数。