记录 LeetCode 第 296 场周赛

本次周赛虽然非常简单，但是依旧仅写出第三题。第一题和第三题花了太长时间，导致第四题没在规定时间内写出来。

战局详情

排名	用户名	得分	完成时间	题目1（3）	题目2（4）	题目3（5）	题目4（6）
2761 / 5721	Juruoer	12	1:06:10	0:20:26	0:28:22	1:06:10

题目及解答

• 题目1
• 题目2
• 题目3
• 题目4

极大极小游戏

6090. 极大极小游戏

给你一个下标从 0 开始的整数数组 nums ，其长度是 2 的幂。

对 nums 执行下述算法：

1. 设 n 等于 nums 的长度，如果 n == 1 ，终止 算法过程。否则，创建 一个新的整数数组 newNums ，新数组长度为 n / 2 ，下标从 0 开始。
2. 对于满足 0 <= i < n / 2 的每个 偶数 下标 i ，将 newNums[i] 赋值 为 min(nums[2 * i], nums[2 * i + 1]) 。
3. 对于满足 0 <= i < n / 2 的每个 奇数 下标 i ，将 newNums[i] 赋值 为 max(nums[2 * i], nums[2 * i + 1]) 。
4. 用 newNums 替换 nums 。
5. 从步骤 1 开始 重复 整个过程。

执行算法后，返回 nums 中剩下的那个数字。

提示：

• 1 <= nums.length <= 1024
• 1 <= nums[i] <= 1e9
• nums.length 是 2 的幂

示例一：

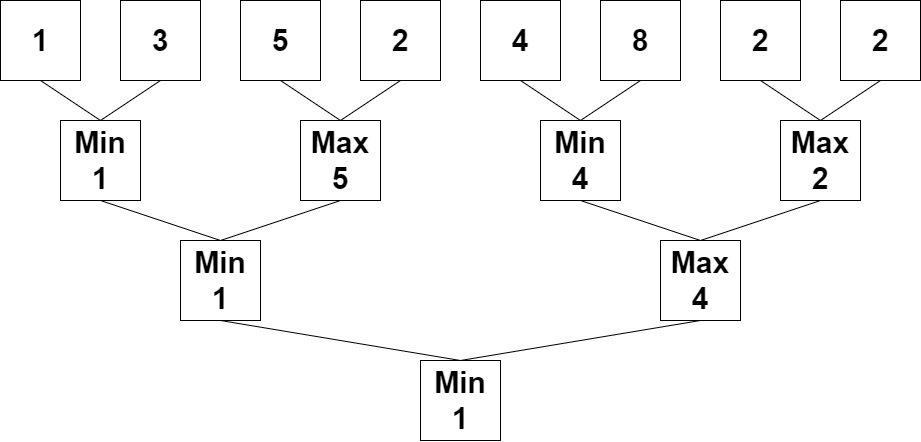
输入：nums = [1,3,5,2,4,8,2,2]
输出：1
解释：重复执行算法会得到下述数组。
第一轮：nums = [1,5,4,2]
第二轮：nums = [1,4]
第三轮：nums = [1]
1 是最后剩下的那个数字，返回 1 。

示例二：

输入：nums = [3]
输出：3
解释：3 就是最后剩下的数字，返回 3 。

解决方案：

很显然这是一个递归，每轮将数组分为等长度的两份，且观察可知，左边这份计算出的值一定位于新数组的偶数下标位，右边这份计算出的值一定位于新数组的奇数下标位。

代码：

class Solution
{
public:
    // 待计算的数组范围，isMin 表示要获得的是否为最小值
    int bin(vector<int> &nums, int l, int r, bool isMin)
    {
        if(l == r)
            return nums[l];
        int _r = (l + r) / 2;
        // 分为两份，左边的 [l, _r] 求最小值，右边的 [_r + 1, r] 求最大值
        return isMin ? min(bin(nums, l, _r, true), bin(nums, _r + 1, r, false)) : max(bin(nums, l, _r, true), bin(nums, _r + 1, r, false));
    }

    int minMaxGame(vector<int> &nums)
    {
        return bin(nums, 0, nums.size() - 1, true);
    }
};

设 nums 长度为 n，遍历了一遍 nums，递归了$\sum _{i = 0} ^{log_2 n} 2 ^ i = 2n - 1$ 次，故时间复杂度为：$O(n)$ ；空间复杂度为：$O(n)$ 。

划分数组使最大差为 K

6091. 划分数组使最大差为 K

给你一个整数数组 nums 和一个整数 k 。你可以将 nums 划分成一个或多个 子序列 ，使 nums 中的每个元素都 恰好 出现在一个子序列中。

在满足每个子序列中最大值和最小值之间的差值最多为 k 的前提下，返回需要划分的 最少 子序列数目。

子序列 本质是一个序列，可以通过删除另一个序列中的某些元素（或者不删除）但不改变剩下元素的顺序得到。

提示：

• 1 <= nums.length <= 1e5
• 0 <= nums[i] <= 1e5
• 0 <= k <= 1e5

示例一：

输入：nums = [3,6,1,2,5], k = 2
输出：2
解释：
可以将 nums 划分为两个子序列 [3,1,2] 和 [6,5] 。
第一个子序列中最大值和最小值的差值是 3 - 1 = 2 。
第二个子序列中最大值和最小值的差值是 6 - 5 = 1 。
由于创建了两个子序列，返回 2 。可以证明需要划分的最少子序列数目就是 2 。

示例二：

输入：nums = [1,2,3], k = 1
输出：2
解释：
可以将 nums 划分为两个子序列 [1,2] 和 [3] 。
第一个子序列中最大值和最小值的差值是 2 - 1 = 1 。
第二个子序列中最大值和最小值的差值是 3 - 3 = 0 。
由于创建了两个子序列，返回 2 。注意，另一种最优解法是将 nums 划分成子序列 [1] 和 [2,3] 。

示例三：

输入：nums = [2,2,4,5], k = 0
输出：3
解释：
可以将 nums 划分为三个子序列 [2,2]、[4] 和 [5] 。
第一个子序列中最大值和最小值的差值是 2 - 2 = 0 。
第二个子序列中最大值和最小值的差值是 4 - 4 = 0 。
第三个子序列中最大值和最小值的差值是 5 - 5 = 0 。
由于创建了三个子序列，返回 3 。可以证明需要划分的最少子序列数目就是 3 。

解决方案：

贪心算法，将 nums 排序，然后让尽可能多的数字在一个子序列中。

代码：

class Solution
{
public:
    int partitionArray(vector<int> &nums, int k)
    {
        sort(nums.begin(), nums.end());
        int t = nums[0] + k;
        int rst = 1;
        for(int num : nums)
        {
            if(num > t)
            {
                rst++;
                t = num + k;
            }
        }
        return rst;
    }
};

时间复杂度为：$O(n)$ ；空间复杂度为：$O(1)$ 。n 为 nums 的长度

替换数组中的元素

6092. 替换数组中的元素

给你一个下标从 0 开始的数组 nums ，它包含 n 个 互不相同 的正整数。请你对这个数组执行 m 个操作，在第 i 个操作中，你需要将数字 operations[i][0] 替换成 operations[i][1] 。

题目保证在第 i 个操作中：

• operations[i][0] 在 nums 中存在。
• operations[i][1] 在 nums 中不存在。

请你返回执行完所有操作后的数组。

提示：

• n == nums.length
• m == operations.length
• 1 <= n, m <= 1e5
• nums 中所有数字 互不相同 。
• operations[i].length == 2
• 1 <= nums[i], operations[i][0], operations[i][1] <= 1e6
• 在执行第 i 个操作时，operations[i][0] 在 nums 中存在。
• 在执行第 i 个操作时，operations[i][1] 在 nums 中不存在。

示例一：

输入：nums = [1,2,4,6], operations = [[1,3],[4,7],[6,1]]
输出：[3,2,7,1]
解释：我们对 nums 执行以下操作：

• 将数字 1 替换为 3 。nums 变为 [3,2,4,6] 。
• 将数字 4 替换为 7 。nums 变为 [3,2,7,6] 。
• 将数字 6 替换为 1 。nums 变为 [3,2,7,1] 。

返回最终数组 [3,2,7,1] 。

示例二：

输入：nums = [1,2], operations = [[1,3],[2,1],[3,2]]
输出：[2,1]
解释：我们对 nums 执行以下操作：

• 将数字 1 替换为 3 。nums 变为 [3,2] 。
• 将数字 2 替换为 1 。nums 变为 [3,1] 。
• 将数字 3 替换为 2 。nums 变为 [2,1] 。

返回最终数组 [2,1] 。

解决方案：

按提议模拟即可

代码：

class Solution
{
public:
    vector<int> arrayChange(vector<int> &nums, vector<vector<int>> &operations)
    {
        unordered_map<int, int> idxs; // 记录每个数字的下标
        for (int i = 0; i < nums.size(); ++i)
            idxs[nums[i]] = i;

        for (auto op : operations)
        {
            // 将 op[0] 替换为 op[1]，且 idxs 中一定存在op[0]，一定不存在op[1]（其实存在op[1]，但是可以假装不存在）
            int idx = idxs[op[0]];
            // 此时可以把 op[0] 从 idxs 中删去，但是不删也没关系
            idxs[op[1]] = idx;
            nums[idx] = op[1];
        }
        return nums;
    }
};

时间复杂度为：$O(m + n)$ ；空间复杂度为：$O(m + n)$，若每次都将 op[0] 从 idxs 中删去，则空间复杂度为$O(n)$ 。m 为 操作次数，n 为 nums 长度。

设计一个文本编辑器

6093. 设计一个文本编辑器

请你设计一个带光标的文本编辑器，它可以实现以下功能：

• 添加：在光标所在处添加文本。
• 删除：在光标所在处删除文本（模拟键盘的删除键）。
• 移动：将光标往左或者往右移动。

当删除文本时，只有光标左边的字符会被删除。光标会留在文本内，也就是说任意时候 0 <= cursor.position <= currentText.length 都成立。

请你实现 TextEditor 类：

• TextEditor() 用空文本初始化对象。
• void addText(string text) 将 text 添加到光标所在位置。添加完后光标在 text 的右边。
• int deleteText(int k) 删除光标左边 k 个字符。返回实际删除的字符数目。
• string cursorLeft(int k) 将光标向左移动 k 次。返回移动后光标左边 min(10, len) 个字符，其中 len 是光标左边的字符数目。
• string cursorRight(int k) 将光标向右移动 k 次。返回移动后光标左边 min(10, len) 个字符，其中 len 是光标左边的字符数目。

提示：

1 <= text.length, k <= 40
text 只含有小写英文字母。
调用 addText ，deleteText ，cursorLeft 和 cursorRight 的 总 次数不超过 2 * 1e4 次。

示例一：

输入：
[“TextEditor”, “addText”, “deleteText”, “addText”, “cursorRight”, “cursorLeft”, “deleteText”, “cursorLeft”, “cursorRight”]
[[], [“leetcode”], [4], [“practice”], [3], [8], [10], [2], [6]]
输出：
[null, null, 4, null, “etpractice”, “leet”, 4, “”, “practi”]

解释：

TextEditor textEditor = new TextEditor(); // 当前 text 为 "|" 。（'|' 字符表示光标）
textEditor.addText("leetcode"); // 当前文本为 "leetcode|" 。
textEditor.deleteText(4); // 返回 4
                          // 当前文本为 "leet|" 。
                          // 删除了 4 个字符。
textEditor.addText("practice"); // 当前文本为 "leetpractice|" 。
textEditor.cursorRight(3); // 返回 "etpractice"
                           // 当前文本为 "leetpractice|". 
                           // 光标无法移动到文本以外，所以无法移动。
                           // "etpractice" 是光标左边的 10 个字符。
textEditor.cursorLeft(8); // 返回 "leet"
                          // 当前文本为 "leet|practice" 。
                          // "leet" 是光标左边的 min(10, 4) = 4 个字符。
textEditor.deleteText(10); // 返回 4
                           // 当前文本为 "|practice" 。
                           // 只有 4 个字符被删除了。
textEditor.cursorLeft(2); // 返回 ""
                          // 当前文本为 "|practice" 。
                          // 光标无法移动到文本以外，所以无法移动。
                          // "" 是光标左边的 min(10, 0) = 0 个字符。
textEditor.cursorRight(6); // 返回 "practi"
                           // 当前文本为 "practi|ce" 。
                           // "practi" 是光标左边的 min(10, 6) = 6 个字符。

解决方案：

因为不需要实时返回文本内容，且多为 添加 和 删除 操作，移动 操作移动距离较短，故使用 链式存储结构 合适。

所以可以使用一个链表来维护文本，然后模拟即可。

代码：

class TextEditor
{
private:
    typedef struct node
    {
        node *next; // 后继
        node *pre; // 前驱
        char c; // 字符

        node(char _c = 0, node *_pre = nullptr)
        {
            c = _c;
            next = nullptr;
            pre = _pre;
        }
    }node;
    node t; // 头节点，指向整个文本
    node *p; // 当前光标指向所在位置的最后一个字符，例如 "abc|d"，'|' 表示光标，则 p 指向 'c'
    int left; // 当前光标前的字符个数

public:
    TextEditor()
    {
        p = &t;
        left = 0;
    }

    void addText(string text)
    {
        node *q = p->next; // q 指向原插入位置后的文本，可能为空
        for(char c : text) // 将待插入的字符插入
        {
            p->next = new node(c, p);
            p = p->next;
        }
        p->next = q; // 接上原插入位置后的文本
        if(q) // 如果原插入位置后存在文本，则重定向其前驱
            q->pre = p;
        left += text.length(); // 当前光标位置改变，其左边字符数增加
    }

    int deleteText(int k)
    {
        node *q = p;
        k = min(k, left); // 此时 k 为实际删除的字符数
        for(int i = 0; i < k; ++i) // 寻找要删除的字符串的前驱
            q = q->pre;

        q->next = p->next; // 删除 q->next 到 p 的所有字符（注意：实际开发时应当释放这些节点的空间）
        if(p->next) // 如果后面还有文本，则重定向其前驱
            p->next->pre = q;
        p = q; // 改变光标位置
        left -= k; // 光标前的字符数减少
        return k;
    }

    string cursorLeft(int k)
    {
        string rst = "";
        k = min(left, k); // 实际左移个数
        for (int i = 0; i < k; ++i) // 光标左移
            p = p->pre;
        
        left -= k; // 光标前字符数减少
        int len = min(left, 10); // 按要求返回的字符串的长度
        node *q = p;
        for (int i = 0; i < len; ++i) // 构建返回的字符串
        {
            rst.insert(0, 1, q->c);
            q = q->pre;
        }
        return rst;
    }

    string cursorRight(int k)
    {
        string rst = "";
        for (int i = 0; i < k; ++i) // 光标右移到指定位置或文本末尾
        {
            if(p->next == nullptr)
                break;
            p = p->next;
            left++; // 光标前字符串增加
        }
        int len = min(left, 10); // 按要求返回的字符串的长度
        node *q = p;
        for (int i = 0; i < len; ++i) // 构建返回的字符串
        {
            rst.insert(0, 1, q->c); 
            q = q->pre;
        }
        return rst;
    }
};


/**
 * Your TextEditor object will be instantiated and called as such:
 * TextEditor* obj = new TextEditor();
 * obj->addText(text);
 * int param_2 = obj->deleteText(k);
 * string param_3 = obj->cursorLeft(k);
 * string param_4 = obj->cursorRight(k);
 */

TextEditor()：时间复杂度为：$O(1)$ ；空间复杂度为：$O(1)$ 。

addText(string text)：时间复杂度为：$O(k)$ ；空间复杂度为：O(k) 。k 为 text 长度。

deleteText(int k)：时间复杂度为：$O(k)$ ；空间复杂度为：$O(1)$ 。k 为删除字符数

cursorLeft(int k)：时间复杂度为：$O(k)$ ；空间复杂度为：$O(1)$ 。k 为移动次数

cursorRight(int k)：时间复杂度为：$O(k)$ ；空间复杂度为：$O(1)$ 。k 为移动次数

总时间复杂度为：$O(k \times c)$ ；空间复杂度为：$O(k \times ac)$，若删除时将空间释放，则空间复杂度可以更小。k 表示每次增加或删除或移动的字符个数，c 表示 总操作次数，ac 表示添加操作的次数。