本次周赛依旧只写出前三题。

战局详情

排名	用户名	得分	完成时间	题目1（3）	题目2（4）	题目3（5）	题目4（6）
639 / 6108	Juruoer	12	0:36:29	0:04:27	0:15:56	0:31:29 1

题目及解答

判断矩阵是否是一个 X 矩阵

2319. 判断矩阵是否是一个 X 矩阵

如果一个正方形矩阵满足下述全部条件，则称之为一个 X 矩阵：

矩阵对角线上的所有元素都 不是 0
矩阵中所有其他元素都是 0

给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ，返回 true ；否则，返回 false 。

提示：

n == grid.length == grid[i].length
3 <= n <= 100
0 <= grid[i][j] <= 1e5

示例一：

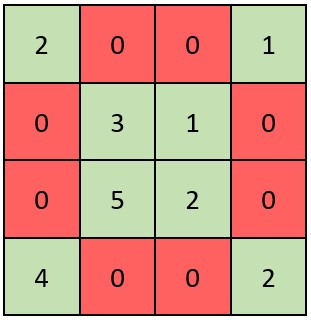
输入：grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出：true
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 是一个 X 矩阵。

示例二：

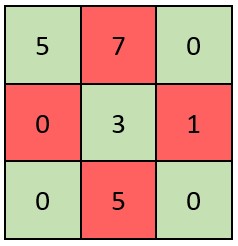
输入：grid = [[5,7,0],[0,3,1],[0,5,0]]
输出：false
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 不是一个 X 矩阵。

解决方案：

模拟：

遍历二维数组（设为 n 行 n 列），若某元素下标 i，j 满足：i == j 或 i + j == n - 1 则为对角线元素，否则为非对角线元素。

代码：

class Solution
{
public:
    bool checkXMatrix(vector<vector<int>> &grid)
    {
        int i, j;
        int n = grid.size();
        for (i = 0; i < n; ++i)
        {
            for (j = 0; j < n; ++j)
            {
                if((i == j) || (i + j == n - 1)) // 对角线元素
                {
                    if(grid[i][j] == 0)
                        return false;
                }
                else
                    if(grid[i][j] != 0)
                        return false;
            }
        }
        return true;
    }
};

时间复杂度： $O(n^2)$ ；空间复杂度： $O(1)$ 。

统计放置房子的方式数

2320. 统计放置房子的方式数

一条街道上共有 n * 2 个地块，街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。

现要求街道同一侧不能存在两所房子相邻的情况，请你计算并返回放置房屋的方式数目。由于答案可能很大，需要对 1e9 + 7 取余后再返回。

注意，如果一所房子放置在这条街某一侧上的第 i 个地块，不影响在另一侧的第 i 个地块放置房子。

提示：

1 <= n <= 1e4

示例一：

输入：n = 1
输出：4
解释：
可能的放置方式：

所有地块都不放置房子。
一所房子放在街道的某一侧。
一所房子放在街道的另一侧。
放置两所房子，街道两侧各放置一所。

示例二：

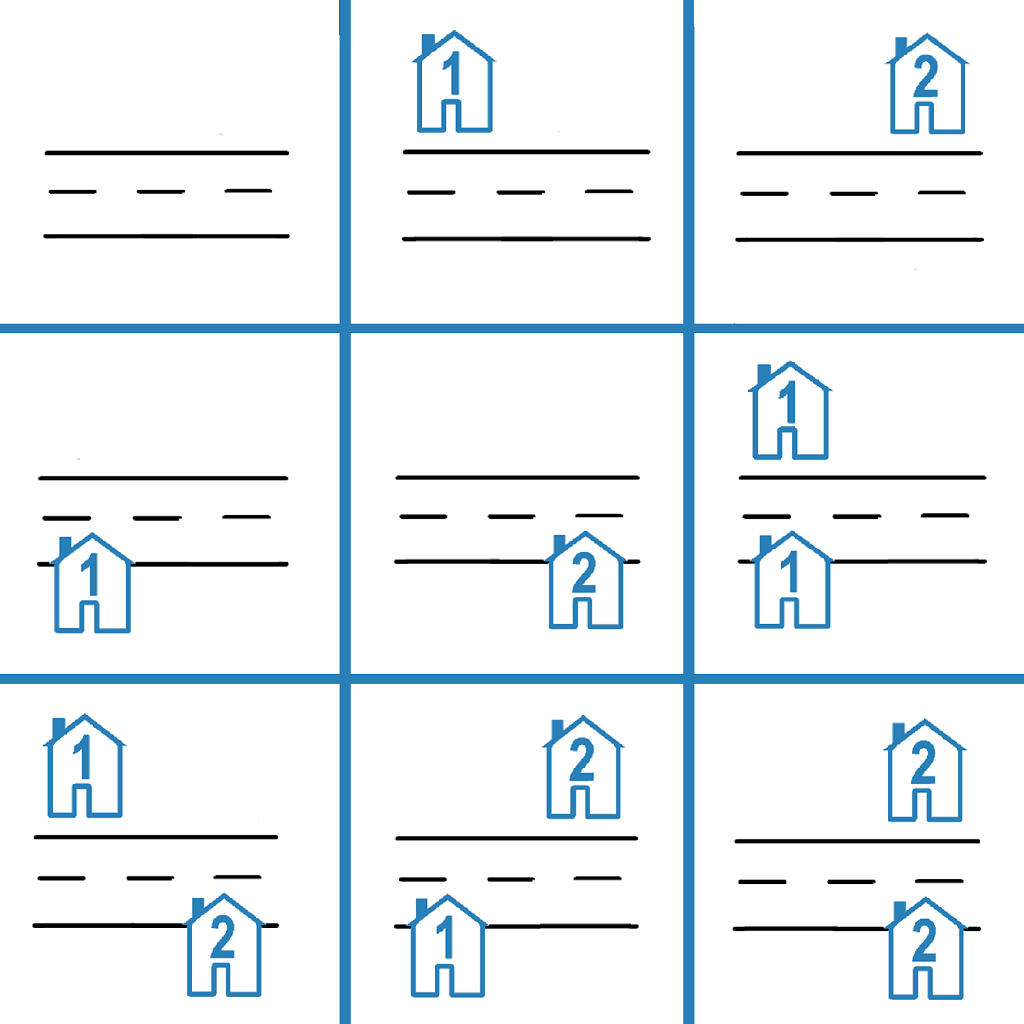
输入：n = 2
输出：9
解释：如上图所示，共有 9 种可能的放置方式。

解决方案：

动态规划：

因为街道一侧的房子并不影响另一侧房子的摆放方式，所以只需要计算出一侧的摆放方式，其平分即为两侧摆放的总方式。

对于某一侧，设：

dp[i][0] 表示自第 0 个地块起到第 i 个地块为止，且第 i 个地块 不摆放 房子的方式数，它是前一个位置摆放房子的方式数和前一个位置不摆放房子的方式数的总和。
dp[i][1] 表示自第 0 个地块起到第 i 个地块为止，且第 i 个地块摆放房子的方式数，它与前一个位置不摆放房子的方式数相同（两所房子不能相邻）。

那么有：

dp[i][0] = dp[i - 1][0] + dp[i - 1][1] 。
dp[i][1] = dp[i - 1][0] 。

代码：

class Solution
{
public:
    int countHousePlacements(int n)
    {
        int dp[n][2];
        int MOD = 1e9 + 7;
        // dp[i][0] = dp[i - 1][0] + dp[i - 1][1]
        // dp[i][1] = dp[i][0]
        dp[0][0] = dp[0][1] = 1;

        for (int i = 1; i < n; ++i)
        {
            dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % MOD;
            dp[i][1] = dp[i - 1][0];
        }

        int x = (dp[n - 1][0] + dp[n - 1][1]) % MOD;
        return (1LL * x * x) % MOD;
    }
};

时间复杂度： $O(n)$ ；空间复杂度： $O(n)$ 。由于 dp[i] 只依赖于 dp[i - 1] ，故空间复杂度可以优化到 $O(1)$ ~~(非常简单就不写了)~~ 。

拼接数组的最大分数

2321. 拼接数组的最大分数

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，长度都是 n 。

你可以选择两个整数 left 和 right ，其中 0 <= left <= right < n ，接着交换两个子数组 nums1[left...right] 和 nums2[left...right] 。

例如，设 nums1 = [1,2,3,4,5] 和 nums2 = [11,12,13,14,15] ，整数选择 left = 1 和 right = 2，那么 nums1 会变为 [1,12,13,4,5] 而 nums2 会变为 [11,2,3,14,15] 。

你可以选择执行上述操作一次或不执行任何操作。

数组的分数取 sum(nums1) 和 sum(nums2) 中的最大值，其中 sum(arr) 是数组 arr 中所有元素之和。

返回 可能的最大分数 。

子数组 是数组中连续的一个元素序列。arr[left...right] 表示子数组包含 nums 中下标 left 和 right 之间的元素（含下标 left 和 right 对应元素）。

提示：

n == nums1.length == nums2.length
1 <= n <= 1e5
1 <= nums1[i], nums2[i] <= 1e4

示例一：

输入：nums1 = [60,60,60], nums2 = [10,90,10]
输出：210
解释：选择 left = 1 和 right = 1 ，得到 nums1 = [60,90,60] 和 nums2 = [10,60,10] 。
分数为 max(sum(nums1), sum(nums2)) = max(210, 80) = 210 。

示例二：

输入：nums1 = [20,40,20,70,30], nums2 = [50,20,50,40,20]
输出：220
解释：选择 left = 3 和 right = 4 ，得到 nums1 = [20,40,20,40,20] 和 nums2 = [50,20,50,70,30] 。
分数为 max(sum(nums1), sum(nums2)) = max(140, 220) = 220 。

示例三：

输入：nums1 = [7,11,13], nums2 = [1,1,1]
输出：31
解释：选择不交换任何子数组。
分数为 max(sum(nums1), sum(nums2)) = max(31, 3) = 31 。

解决方案：

动态规划：

分为两种情况：

最终结果为 nums2 的子数组被交换到了 nums1 中。
最终结果为 nums1 的子数组被交换到了 nums2 中。

这两种情况隐含了没有交换子数组的情况。

我们先研究第一种情况：

朴素的想法是，我们枚举出所有的子数组范围，然后挨个计算交换后 nums1 的元素和，取最大值。但是其中有一些范围，若我们交换后 nums1 元素和反而减少了，这种情况是可以优化排除掉的。

应当找出所有交换后 nums1 元素和增大的情况，可以使用双指针法：

设某个范围起点为 i ，终点为 j，不断增加 j 以扩大交换范围，并在此过程中计算每一次 j 变化后的 nums2 和 nums1 在该范围的元素和的差值，记录最大的差值，直到某次增加 j 后，差值为负，说明该范围 nums2 的元素和小于 nums1 的元素和，那么以 i 为起点的范围便就此结束，最终的结果的范围一定不会是自 i 到此时 j 之后的范围（但可能是 i 到 j 之前的某个范围，所以我们需要记录每次 j 增加后的差值，取最大值），因为范围 i 到 j 已然相当于一个累赘，之后的范围加上这个范围，差值只会更小，所以要从 j 处开始新的范围了（即令 i = j）。

这个过程中 i 是可以不显式的表示出来的。

若 dp[j] 表示 i （i 在什么位置无需知道）到 j 范围内交换元素，nums1 可以获得的增量，任何情况下 dp[j] >= 0 ，当增量为负时，范围起点变为 j 增量变为 0 相当于不交换元素的增量。在此过程中，用 _max 记录最大的增量。则有：

dp[j] = max(dp[j - 1] + (nums2[j] - nums1[j]), 0);
_max = _max(_max, dp[j]);

同理，第二种情况也是如此。

由于 dp[j] 只依赖 dp[j - 1] ，所以可以使用一个 int dp 来优化空间。

代码：

class Solution
{
public:
    int maximumsSplicedArray(vector<int> &nums1, vector<int> &nums2)
    {
        int sum1 = accumulate(nums1.begin(), nums1.end(), 0); // nums1 的元素和
        int sum2 = accumulate(nums2.begin(), nums2.end(), 0); // nums2 的元素和
        int i, n = nums1.size();
        int dp1, dp2;
        // dp1 和 max1 记录情况一，dp2 和 max2 记录情况二
        dp1 = max(nums2[0] - nums1[0], 0);
        dp2 = max(nums1[0] - nums2[0], 0);
        int max1, max2;
        max1 = dp1;
        max2 = dp2;
        for (i = 1; i < n; ++i) // 范围自 i 之前的某个位置到 i（此处 i 为上述分析的 j）
        {
            dp1 = max(dp1 + (nums2[i] - nums1[i]), 0); // 当 dp1 + (nums2[i] - nums1[i]) < 0 时，即是改变范围起点之时，新的范围开始时，dp1 = 0
            dp2 = max(dp2 + (nums1[i] - nums2[i]), 0); // dp2 同理
            max1 = max(max1, dp1); // 在此过程中更新最大的差值
            max2 = max(max2, dp2);
        }
        return max(sum1 + max1, sum2 + max2);
    }
};

时间复杂度： $O(n)$ ；空间复杂度为： $O(1)$ 。n 为数组长度。

从树中删除边的最小分数

2322. 从树中删除边的最小分数

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点，以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条不同的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

分别获取三个组件每个组件中所有节点值的异或值。
最大异或值和 最小Z 异或值的差值就是这一种删除边方案的分数。

例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。
返回在给定树上执行任意删除边方案可能的最小分数。

提示：

n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 1e8
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵有效的树

示例一：

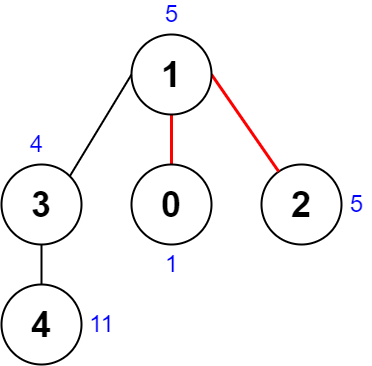
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：9
解释：上图展示了一种删除边方案。

第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。

分数是最大异或值和最小异或值的差值，10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。

示例二：

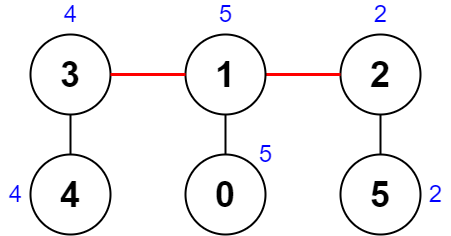
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出：0
解释：上图展示了一种删除边方案。

第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。

分数是最大异或值和最小异或值的差值，0 - 0 = 0 。
无法获得比 0 更小的分数 0 。

解决方案：
DFS：

本方法参考至大佬灵茶山艾府的题解。

首先为无向连通图设立一个根节点，假设为 0 节点。

对于这棵树，可以通过 dfs 算法来计算各个子树的异或值（假设 _xor[i] 为以 i 为根节点的子树的异或值），然后遍历所有可能的删边情况，计算各种情况下的分数。

假设删除了两条边： x1-y1 和 x2-y2，其中 x1 为 y1 的父节点，x2 为 y2 的父节点，那么我们就将树大体分为了三部分，以 y1 为根节点的子树 tree[y1]，以 y2 为根节点的子树 tree[y2] ，树的其他部分 tree[0] - （tree[y1] ∪ tree[y2]） 。但还有一个问题，tree[y1] 和 tree[y2] 可能有交集，也就是说 tree[y1] 可能是 tree[y2] 的子树，或者相反。我们先不管如何判断谁是谁的子树，先给出各种情况下各部分的异或值，设三部分的异或值分别为 x 、y 、z：

tree[y1] 是 tree[y2] 的子树：x = _xor[y1], y = _xor[y2] ^ x, z = _xor[0] ^ _xor[y2]` 。
tree[y2] 是 tree[y1] 的子树：x = _xor[y2], y = _xor[y1] ^ x, z = _xor[0] ^ _xor[y1]` 。
tree[y2] 和 tree[y1] 没有交集：x = _xor[y1], y = _xor[y2], z = _xor[0] ^ x ^ y;

那么当前的问题便被转化为如何判断 y1 和 y2 的从属关系。若是使用并查集或遍历的方法时间复杂度太高，能否用 $O(1)$ 时间复杂度来判断呢？答案是可以，使用时间戳来判断。

由于之前是通过 dfs 来计算各个子树的异或值的，所以可以标记递归到每个节点时的递归进入时间戳和递归结束时间戳，假设 in[i] 表示递归到 i 节点时的时间戳，out[i] 表示 i 节点递归结束时的时间戳，倘若：

in[i] < in[j] < out[j] < out[i]，那么表明对 j 的递归是在对 i 的递归的过程中完成的，也就是说，j 是 i 的子孙节点，由递归的过程可知，当满足 in[i] < in[j] < out[i] 时一定满足 out[j] < out[i] 。

代码：

class Solution
{
private:
    vector<int> in; // in[i] 表示第 i 个点递归起始时间戳
    vector<int> out; // out[i] 表示第 i 个点递归结束时间戳
    // 对于节点 i 和节点 j，若 in[i] < in[j] < out[j] < out[i] 则 i 为 j 的祖先节点，可简化为：in[i] < in[j] < out[j]
    vector<int> _xor; // _xor[i] 表示以节点 i 为根节点的子树的异或值
    vector<vector<int>> g; // g[i] 表示于 i 直接相连的点集
    int clock = 0; // 计时器

    void dfs(int root, int par, vector<int> &nums)
    {
        in[root] = ++clock; // 记录进入时间戳
        _xor[root] = nums[root];
        for(auto &ch : g[root]) // 对于所有与 root 相连的点
        {
            if(ch != par) // 若该点不是 root 父节点
            {
                dfs(ch, root, nums);
                _xor[root] ^= _xor[ch];
            }
        }
        out[root] = ++clock; // 记录结束时间戳
    }

public:
    int minimumScore(vector<int> &nums, vector<vector<int>> &edges)
    {
        int n = nums.size();
        in.resize(n);
        out.resize(n);
        _xor.resize(n);
        g.resize(n);

        for (auto &e : edges)
        {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        // 以 0 为根节点，计算树中各子树的异或值
        dfs(0, -1, nums);

        int i, j; // 以节点 i 和节点 j 为根的子树独立出来，相当于在原树上删除两条边
        int x, y, z, ans = 0x7fffffff;
        for (i = 2; i < n; ++i) // 选定以 i 为根节点子树，删除点 i 和其父节点的边
        {
            for (j = 1; j < i; ++j) // 选定以 j 为根节点子树，删除点 j 和其父节点的边
            {
                if((in[i] < in[j] && in[j] < out[i])) // j 是 i 的子树
                {
                    x = _xor[j]; // 子树 j 的异或值
                    y = _xor[i] ^ x; // 子树 i 去除子树 j 的异或值
                    z = _xor[0] ^ _xor[i]; // 树去除子树 i 的异或值
                }
                else if(in[j] < in[i] && in[i] < out[j]) // i 是 j 的子树
                {
                    x = _xor[i]; // 子树 i 的异或值
                    y = _xor[j] ^ x; // 子树 j 去除子树 i 的异或值
                    z = _xor[0] ^ _xor[j]; // 树去除子树 j 的异或值
                }
                else{ // 两棵没有交集的子树
                    x = _xor[i]; // 子树 i 的异或值
                    y = _xor[j]; // 子树 j 的异或值
                    z = _xor[0] ^ x ^ y; // 树去除子树 i 和子树 j 的异或值
                }
                ans = min(ans, (max(x, max(y, z)) - min(x, min(y, z))));
                if (ans == 0) // 不可能有比 0 更小的结果
                    return 0;
            }
        }

        return ans;
    }
};

时间复杂度： $O(m + n ^ 2)$ ；g 的大小和边数正比，其他数组大小同 n，空间复杂度： $O(m + n)$ 。m 为边，n 为节点数。

记录 LeetCode 第 299 场周赛

战局详情

题目及解答