本次周赛 十分可惜，很有可能 AK 的比赛却仅写出前两题。第三题带错了一个动态规划初始值，第四题没看题目，赛后十分钟给 AC 了。

战局详情

排名用户名得分完成时间题目1（3）题目2（4）题目3（5）题目4（6）
2385 / 6792Juruoer70:29:560:10:570:24:56 1

题目及解答

解密消息

6108. 解密消息

给你字符串 key 和 message ，分别表示一个加密密钥和一段加密消息。解密 message 的步骤如下：

  1. 使用 key 中 26 个英文小写字母第一次出现的顺序作为替换表中的字母 顺序 。

  2. 将替换表与普通英文字母表对齐，形成对照表。

  3. 按照对照表 替换 message 中的每个字母。

  4. 空格 ' ' 保持不变。

  • 例如，key = "happy boy"（实际的加密密钥会包含字母表中每个字母 至少一次），据此，可以得到部分对照表（'h' -> 'a'、'a' -> 'b'、'p' -> 'c'、'y' -> 'd'、'b' -> 'e'、'o' -> 'f'）。

返回解密后的消息。

提示：

  • 26 <= key.length <= 2000
  • key 由小写英文字母及 ' ' 组成
  • key 包含英文字母表中每个字符（'a' 到 'z'）至少一次
  • 1 <= message.length <= 2000
  • message 由小写英文字母和 ' ' 组成

示例一：

示例一图

输入：key = “the quick brown fox jumps over the lazy dog”, message = “vkbs bs t suepuv”
输出：“this is a secret”
解释：对照表如上图所示。
提取 “the quick brown fox jumps over the lazy dog” 中每个字母的首次出现可以得到替换表。

示例二：

示例二图

输入：key = “eljuxhpwnyrdgtqkviszcfmabo”, message = “zwx hnfx lqantp mnoeius ycgk vcnjrdb”
输出：“the five boxing wizards jump quickly”
解释：对照表如上图所示。
提取 “eljuxhpwnyrdgtqkviszcfmabo” 中每个字母的首次出现可以得到替换表。

解决方案：

模拟 + 映射：

使用一个数组来映射每个字母转换后的字母，然后模拟即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution
{
public:
    string decodeMessage(string key, string message)
    {
        char c = 'a';
        vector<char> to(26, ' '); // 映射数组，字母 i + 'a' 被映射到 to[i]
        for(char k : key) // 构建映射数组
        {
            if (k == ' ' || to[k - 'a'] != ' ')
                continue;
            to[k - 'a'] = c;
            if (c == 'z')
                break;
            ++c;
        }
        string rst;
        // 模拟替换
        for(char k : message)
        {
            if(k == ' ')
                rst.push_back(k);
            else
                rst.push_back(to[k - 'a']);
        }
        return rst;
    }   
};

时间复杂度：O(n1+n2)O(n1 + n2) ；空间复杂度：O(c+n1)O(c + n1) 。c 为字母种类数，为 26 ，n1 为 message 长度，n2 为 key 长度。

螺旋矩阵 IV

6111. 螺旋矩阵 IV

给你两个整数：m 和 n ，表示矩阵的维数。

另给你一个整数链表的头节点 head 。

请你生成一个大小为 m x n 的螺旋矩阵，矩阵包含链表中的所有整数。链表中的整数从矩阵 左上角 开始、顺时针 按 螺旋 顺序填充。如果还存在剩余的空格，则用 -1 填充。

返回生成的矩阵。

提示：

  • 1 <= m, n <= 1e5
  • 1 <= m * n <= 1e5
  • 链表中节点数目在范围 [1, m * n] 内
  • 0 <= Node.val <= 1000

示例一：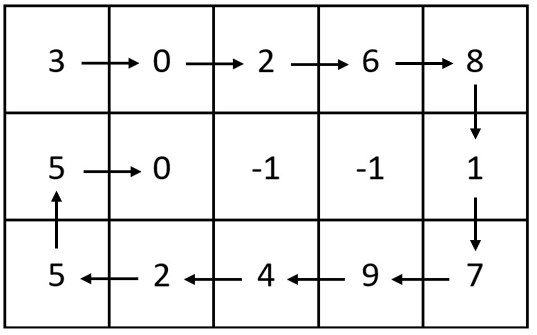
示例一图

输入：m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
输出：[[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
解释：上图展示了链表中的整数在矩阵中是如何排布的。
注意，矩阵中剩下的空格用 -1 填充。

示例二：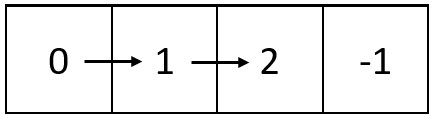
示例一图

输入：m = 1, n = 4, head = [0,1,2]
输出：[[0,1,2,-1]]
解释：上图展示了链表中的整数在矩阵中是如何从左到右排布的。
注意，矩阵中剩下的空格用 -1 填充。

解决方案：

模拟：

本题同 LeetCode 上 59. 螺旋矩阵 II 。只需修改数据的流向即可。这里仅给出我的代码做参考。（但其实我这个写的有点复杂，不是很好描述，有很多更清晰明了的解法可以去 LeetCode 上查找。）

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Solution
{
public:
    vector<vector<int>> spiralMatrix(int m, int n, ListNode *head)
    {
        vector<vector<int>> matrix(m, vector<int>(n, -1));
        int stepi = m;
        int stepj = n;
        int cnt;
        int i, j, dir; // dir表示方向，0为右，1为下，2为左，3为上
        i = dir = 0;
        j = -1;
        --stepi;
        while (head)
        {
            cnt = 0;
            switch (dir)
            {
            case 0: //右
                while (head && cnt < stepj)
                {
                    matrix[i][++j] = head->val;
                    head = head->next;
                    ++cnt;
                }
                --stepj;
                break;
            case 1: //下
                while (head && cnt < stepi)
                {
                    matrix[++i][j] = head->val;
                    head = head->next;
                    ++cnt;
                }
                --stepi;
                break;
            case 2: //左
                while (head && cnt < stepj)
                {
                    matrix[i][--j] = head->val;
                    head = head->next;
                    ++cnt;
                }
                --stepj;
                break;
            case 3:
                while (head && cnt < stepi)
                {
                    matrix[--i][j] = head->val;
                    head = head->next;
                    ++cnt;
                }
                --stepi;
                break;
            default:
                break;
            }
            ++dir;
            dir %= 4;
        }
        return matrix;
    }
};

时间复杂度：O(m×n)O(m \times n) ，空间复杂度：O(1)O(1) 。matrix 算结果数组不计入额外空间复杂度。

知道秘密的人数

6109. 知道秘密的人数

在第 1 天，有一个人发现了一个秘密。

给你一个整数 delay ，表示每个人会在发现秘密后的 delay 天之后，每天Z 给一个新的人 分享 秘密。同时给你一个整数 forget ，表示每个人在发现秘密 forget 天之后会 忘记 这个秘密。一个人 不能 在忘记秘密那一天及之后的日子里分享秘密。

给你一个整数 n ，请你返回在第 n 天结束时，知道秘密的人数。由于答案可能会很大，请你将结果对 1e9 + 7 取余 后返回。

提示：

  • 2 <= n <= 1000
  • 1 <= delay < forget <= n

示例一：

输入：n = 6, delay = 2, forget = 4
输出：5
解释：

  • 第 1 天：假设第一个人叫 A 。（一个人知道秘密）
  • 第 2 天：A 是唯一一个知道秘密的人。（一个人知道秘密）
  • 第 3 天：A 把秘密分享给 B 。（两个人知道秘密）
  • 第 4 天：A 把秘密分享给一个新的人 C 。（三个人知道秘密）
  • 第 5 天：A 忘记了秘密，B 把秘密分享给一个新的人 D 。（三个人知道秘密）
  • 第 6 天：B 把秘密分享给 E，C 把秘密分享给 F 。（五个人知道秘密）

示例二：

输入：n = 4, delay = 1, forget = 3
输出：6
解释：

  • 第 1 天：第一个知道秘密的人为 A 。（一个人知道秘密）
  • 第 2 天：A 把秘密分享给 B 。（两个人知道秘密）
  • 第 3 天：A 和 B 把秘密分享给 2 个新的人 C 和 D 。（四个人知道秘密）
  • 第 4 天：A 忘记了秘密，B、C、D 分别分享给 3 个新的人。（六个人知道秘密）

解决方案：

动态规划：

本题动态规划的写法有好多中，其中时间复杂度 O(n^2) 的比较简单，此处给出我的时间复杂度 O(n) 的解法（也还有其他不错O(n)O(n) 的解法）。

首先有如下几条显而易见的递推关系：

  • 第 i 天知道秘密的人数 = 第 i - 1 天知道秘密的人数 - 第 i 天新忘记秘密的人数 + 第 i 天新知道秘密的人数。
  • 第 i 天新忘记秘密的人数 = 在第 i - forget 天新知道秘密的人数（只有这些人刚好过了 forget 天到达第 i 天）。
  • 第 i 天新知道秘密的人数 = 第 i - delay 天所有知道秘密的人数 - 从第 i - delay 天之后所有忘记秘密的人数（因为 forget > delay 所以所有在第 i - delay 天之后忘记秘密的人在第 i - delay 天都记得秘密，而其他没有忘记秘密的人则是第 i 天可以传播秘密的人）。
  • 第 i 天为止所有忘记秘密的人数 = 第 i - 1 天所有忘记秘密的人数 + 第 i 天新忘记秘密的人数。

我们维护三个数组：

  • dp[i] 表示第 i 天知道秘密的人数。
  • f[i] 表示到第 i 天为止所有忘记秘密的人数。
  • k[i] 表示第 i 天新知道秘密的人数。

那么有：

  • f[i] = f[i - 1] + k[i - forget] 。
  • k[i] = dp[i - delay] - (f[i] - f[i - delay]) 。
  • dp[i] = dp[i - 1] - k[i - forget] + k[i] 。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution
{
public:
    int peopleAwareOfSecret(int n, int delay, int forget)
    {
        int MOD = 1e9 + 7;
        int f[n + 1];
        // f[i] = 到第 i 天为止所有忘记秘密的人数
        int k[n + 1];
        // k[i] = 第 i 天新知道秘密的人数
        int dp[n + 1];
        // dp[i] = 第 i 天知道秘密的人数
        // dp[i] = dp[i - 1] - 第 i 天新忘记秘密的人数 + 第 i 天新知道秘密的人数
        // 第 i 天新忘记秘密的人数 = 第 i - forget 天增加的知道秘密的人数
        // 第 i 天新知道秘密的人数 = 第 i - delay 天所有知道秘密的人数 - 从第 i - delay 天之后所有忘记秘密的人数
        // 第 i 天为止所有忘记秘密的人数 = 第 i - 1 天所有忘记秘密的人数 + 第 i 天新忘记秘密的人数

        // f[i] = f[i - 1] + k[i - forget]
        // k[i] = dp[i - delay] - (f[i] - f[i - delay])
        // dp[i] = dp[i - 1] - k[i - forget] + k[i]
        dp[1] = 1;
        f[1] = 0;
        k[1] = 1;
        int d;
        for (int i = 2; i <= n; ++i)
        {
            f[i] = f[i - 1];
            if(i > forget)
                f[i] = (f[i] + k[i - forget]) % MOD;

            k[i] = 0;
            if(i > delay)
                k[i] = (dp[i - delay] - (f[i] - f[i - delay] + MOD) % MOD + MOD) % MOD;

            dp[i] = (dp[i - 1] + k[i]) % MOD;
            if(i > forget)
                dp[i] = (dp[i] - k[i - forget] + MOD) % MOD;
        }
        return dp[n];
    }
};

时间复杂度：O(n)O(n) ；空间复杂度：O(n)O(n) 。

网格图中递增路径的数目

6110. 网格图中递增路径的数目

给你一个 m x n 的整数网格图 grid ，你可以从一个格子移动到 4 个方向相邻的任意一个格子。

请你返回在网格图中从 任意 格子出发，达到 任意 格子，且路径中的数字是 严格递增 的路径数目。由于答案可能会很大，请将结果对 1e9 + 7 取余 后返回。

如果两条路径中访问过的格子不是完全相同的，那么它们视为两条不同的路径。

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 1000
  • 1 <= m * n <= 1e5
  • 1 <= grid[i][j] <= 1e5

示例一：

示例一图

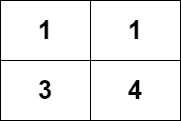
输入：grid = [[1,1],[3,4]]
输出：8
解释：严格递增路径包括：

  • 长度为 1 的路径：[1]，[1]，[3]，[4] 。
  • 长度为 2 的路径：[1 -> 3]，[1 -> 4]，[3 -> 4] 。
  • 长度为 3 的路径：[1 -> 3 -> 4] 。

路径数目为 4 + 3 + 1 = 8 。

示例二：
输入：grid = [[1],[2]]
输出：3
解释：严格递增路径包括：

  • 长度为 1 的路径：[1]，[2] 。
  • 长度为 2 的路径：[1 -> 2] 。

路径数目为 2 + 1 = 3 。

解决方案：

DFS 记忆化搜索：

设 dp[i][j] 表示以 grid[i][j] 为终点的路径数，那么可以递归计算 grid[i][j] 四个方向上所有值小于其的格子的路径数。若某个格子的路径数已经计算完毕，则下次递归到它的时候可以直接返回 dp 。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution
{
private:
    int MOD = 1e9 + 7;
    vector<vector<int>> dp;
    int m, n;
    int dir[4][2] = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
    void dfs(vector<vector<int>> &grid, int x, int y)
    {
        dp[x][y] = 1; // 自身长度为 1 的路径
        for (int i = 0; i < 4; ++i) // 遍历四个方向上的格子
        {
            int nx = x + dir[i][0];
            int ny = y + dir[i][1];
            if(nx >=0 && nx < m && ny >=0 && ny < n && grid[nx][ny] < grid[x][y]) // 满足条件的前驱格子
            {
                if(dp[nx][ny] == 0) // 若没有计算过就计算它
                    dfs(grid, nx, ny);
                dp[x][y] = (dp[x][y] + dp[nx][ny]) % MOD;
            }
        }
    }
public:
    int countPaths(vector<vector<int>> &grid)
    {
        m = grid.size();
        n = grid[0].size();
        dp = vector<vector<int>>(m, vector<int>(n, 0)); // 初始化为 0 而不是 1 的作用是判断该格子的路径数是否已经计算过了
        int i, j, rst = 0;
        for (i = 0; i < m; ++i) // 计算以 grid[i][j] 为终点的路径数
        {
            for (j = 0; j < n; ++j)
            {
                if(dp[i][j] == 0) // 若没有计算过就计算它
                    dfs(grid, i, j);
                rst = (rst + dp[i][j]) % MOD; // 最终结果是所有路径的总和
            }
        }
        return rst;
    }
};

dp[i][j] 只计算一次，时间复杂度：O(m×n)O(m \times n) ；空间复杂度：O(m×n)O(m \times n) 。