本次周赛虽然不难，但仅写出前三题，比赛结束 2 分钟后才写完第四题。

战局详情

排名	用户名	得分	完成时间	题目1（3）	题目2（4）	题目3（5）	题目4（6）
412 / 3028	Juruoer	12	0:55:21	0:10:13	0:30:21	0:45:21 2

题目及解答

使数组成为递增数组的最少右移次数

8039. 使数组成为递增数组的最少右移次数

给你一个长度为 n 下标从 0 开始的数组 nums ，数组中的元素为 互不相同 的正整数。请你返回让 nums 成为递增数组的 最少右移 次数，如果无法得到递增数组，返回 -1 。

一次右移指的是同时对所有下标进行操作，将下标为 i 的元素移动到下标 (i + 1) % n 处。

提示：

1 <= nums.length <= 100
1 <= nums.length <= 100
nums 中的整数互不相同。

示例一：

输入：nums = [3,4,5,1,2]
输出：2
解释：
第一次右移后，nums = [2,3,4,5,1] 。
第二次右移后，nums = [1,2,3,4,5] 。
现在 nums 是递增数组了，所以答案为 2 。

示例二：

输入：nums = [1,3,5]
输出：0
解释：nums 已经是递增数组了，所以答案为 0

示例三：

输入：nums = [2,1,4]
输出：-1
解释：无法将数组变为递增数组。

解决方案：

仅有两种可能能得到递增数组：

整个数组本身递增，此时无需右移。
整个数组可以分为前后两个递增数组，并且后一个递增数组的最后一个元素小于前一个递增数组的第一个元素，此时需要将后一个递增数组移动到前一个递增数组前面，即移动 后一个递增数组的长度 次。

代码：

class Solution {
public:
    int minimumRightShifts(vector<int>& nums) {
        int i = 1;
        for(; i < nums.size(); ++i)
            if(nums[i] < nums[i - 1])
                break;
        if(i == nums.size())  // 整个数组本身递增，无需右移。
            return 0;
        if(nums[0] < nums[nums.size() - 1])  // 即便可以分为两个递增数组，但后一个递增数组的最后一个元素大于前一个递增数组的第一个元素
            return -1;
        int rst = nums.size() - i;
        for(++i; i < nums.size(); ++i)
            if(nums[i] < nums[i - 1])  // 无法分为两个递增数组
                return -1;
        return rst;
    }
};

时间复杂度： $O(n)$ ；空间复杂度： $O(1)$ 。 n 为 nums 的长度。

删除数对后的最小数组长度

2856. 删除数对后的最小数组长度

给你一个下标从 0 开始的 非递减 整数数组 nums 。

你可以执行以下操作任意次：

选择两个下标 i 和 j ，满足 i < j 且 nums[i] < nums[j] 。
将 nums 中下标在 i 和 j 处的元素删除。剩余元素按照原来的顺序组成新的数组，下标也重新从 0 开始编号。
请你返回一个整数，表示执行以上操作任意次后（可以执行 0 次），nums 数组的最小数组长度。

提示：

1 <= nums.length <= 1e5
1 <= nums[i] <= 1e9
nums 是 非递减 数组。

示例一：

输入：nums = [1,3,4,9]
输出：0
解释：一开始，nums = [1, 3, 4, 9] 。
第一次操作，我们选择下标 0 和 1 ，满足 nums[0] < nums[1] <=> 1 < 3 。
删除下标 0 和 1 处的元素，nums 变成 [4, 9] 。
下一次操作，我们选择下标 0 和 1 ，满足 nums[0] < nums[1] <=> 4 < 9 。
删除下标 0 和 1 处的元素，nums 变成空数组 [] 。
所以，可以得到的最小数组长度为 0 。

示例二：

输入：nums = [2,3,6,9]
输出：0
解释：一开始，nums = [2, 3, 6, 9] 。
第一次操作，我们选择下标 0 和 2 ，满足 nums[0] < nums[2] <=> 2 < 6 。
删除下标 0 和 2 处的元素，nums 变成 [3, 9] 。
下一次操作，我们选择下标 0 和 1 ，满足 nums[0] < nums[1] <=> 3 < 9 。
删除下标 0 和 1 处的元素，nums 变成空数组 [] 。
所以，可以得到的最小数组长度为 0 。

示例三：

输入：nums = [1,1,2]
输出：1
解释：一开始，nums = [1, 1, 2] 。
第一次操作，我们选择下标 0 和 2 ，满足 nums[0] < nums[2] <=> 1 < 2 。
删除下标 0 和 2 处的元素，nums 变成 [1] 。
无法对数组再执行操作。
所以，可以得到的最小数组长度为 1 。

解决方案：

一、贪心：

每次选择数量最多的两个不同的数字删除。可以使用堆来维护不同数字的个数。

代码：

class Solution {
public:
    int minLengthAfterRemovals(vector<int>& nums) {
        priority_queue<int> cnts;  // 存放不同数字的个数
        int pre = nums[0];
        int cnt = 0;
        for(int i = 0; i < nums.size(); ++i)
        {
            if(nums[i] == pre)
                ++cnt;
            else
            {
                pre = nums[i];
                cnts.push(cnt);
                cnt = 1;
            }
        }
        cnts.push(cnt);
        int rst = nums.size();
        while(cnts.size() > 1)  // 如果存在两个以上的不同的数字
        {
            int top1 = cnts.top() - 1;  // 最多的数字的个数
            cnts.pop();
            int top2 = cnts.top() - 1;  // 次多的数字的个数
            cnts.pop();
            if(top1 > 0)
                cnts.push(top1);
            if(top2 > 0)
                cnts.push(top2);
            rst -= 2;
        }
        return rst;
    }
};

时间复杂度： $O(nlogn)$ ；空间复杂度： $O(n)$ 。n 为 nums 的长度。

二、贪心优化

研究上面的代码会发现，最终会有两种情况：

存在一个个数最多的数字，出现了 $k$ 次，并且 $k \ge \lfloor \frac{n}{2} \rfloor$ ，那么上述代码中每一次的 top1都是该数剩余的数量，也就是说这个数可以和其他所有数配对删除，并且有可能有剩余。此时的结果为 $n - (n - k) \times 2$
存在一个个数最多的数字，出现了 $k$ 次，并且 $k < \lfloor \frac{n}{2} \rfloor$ ，那么可以被一直配对，直至只剩一个数或全被配对完，此时结果为 $n \mod 2$ 。

代码：

class Solution {
public:
    int minLengthAfterRemovals(vector<int>& nums) {
        int n = nums.size();
        vector<int> cnts;
        int pre = nums[0], cnt = 0;
        for(int i = 0; i < n; ++i)
        {
            if(nums[i] == pre)
                ++cnt;
            else
            {
                pre = nums[i];
                cnts.push_back(cnt);
                cnt = 1;
            }
        }
        cnts.push_back(cnt);
        int t = *max_element(cnts.begin(), cnts.end());
        return t * 2 < n ? n % 2 : n - (n - t) * 2;
    }
};

时间复杂度： $O(n)$ ；空间复杂度： $O(n)$ 。n 为 nums 的长度。

统计距离为 k 的点对

6988. 统计距离为 k 的点对

给你一个二维整数数组 coordinates 和一个整数 k ，其中 coordinates[i] = [xi, yi] 是第 i 个点在二维平面里的坐标。

我们定义两个点 (x1, y1) 和 (x2, y2) 的距离为 (x1 XOR x2) + (y1 XOR y2) ，XOR 指的是按位异或运算。

请你返回满足 i < j 且点 i 和点 j之间距离为 k 的点对数目。

提示：

2 <= coordinates.length <= 50000
0 <= xi, yi <= 1e6
0 <= k <= 100

示例一：

输入：coordinates = [[1,2],[4,2],[1,3],[5,2]], k = 5
输出：2
解释：以下点对距离为 k ：

(0, 1)：(1 XOR 4) + (2 XOR 2) = 5 。
(2, 3)：(1 XOR 5) + (3 XOR 2) = 5 。

示例二：

输入：coordinates = [[1,3],[1,3],[1,3],[1,3],[1,3]], k = 0
输出：10
解释：任何两个点之间的距离都为 0 ，所以总共有 10 组点对。

解决方案：

逆向思维 + 哈希表

由于 coordinates 的长度过长，如果直接暴力会超时，但可以对每个坐标，去寻找满足条件的另一个坐标。

对于坐标 (x1, y1)和 (x2, y2)，若 (x1 XOR x2) = left ，(y1 XOR y2) = right = k - left ，则 x2 = x1 XOR left ，y2 = y1 XOR right，现在的问题是，coordinates 中除去 (x1, y1) 后有多少个 (x2, y2)（因为可能 x1 = x2 且 y1 = y2），可以使用哈希表来记录每个坐标的个数。

如此累计出来的结果可能重复计算（在 (x1, y1) 去寻找 (x2, y2) 后还会出现 (x2, y2) 去寻找 (x1, y1)），所以结果要除以 2。

代码：

class Solution {
public:
    int countPairs(vector<vector<int>>& coordinates, int k) {
        unordered_map<long long, int> map;  // 记录每个坐标出现了多少次
        long long rst = 0;
        for(auto &t : coordinates)
            map[t[0] * 1000000L + t[1]]++;
        for(auto &t : coordinates)  // 遍历每个坐标
        {
            for(int left = 0; left <= k; ++left)  // 遍历每对 (left, right)
            {
                int right = k - left;
                int x = left ^ t[0], y = right ^ t[1];  // 目标坐标
                int cnt = map[x * 1000000L + y] - (x == t[0] && y == t[1]);
                    rst += cnt;
            }
        }
        return rst / 2;  // 会重复计算，结果除以 2
    }
};

时间复杂度： $O(n \times k)$ ；空间复杂度： $O(n)$ ，n 为 coordinates 的长度。

可以到达每一个节点的最少边反转次数

100041. 可以到达每一个节点的最少边反转次数

给你一个 n 个点的 简单有向图 （没有重复边的有向图），节点编号为 0 到 n - 1 。如果这些边是双向边，那么这个图形成一棵树。

给你一个整数 n 和一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示从节点 ui 到节点 vi 有一条 有向边 。

边反转 指的是将一条边的方向反转，也就是说一条从节点 ui 到节点 vi 的边会变为一条从节点 vi 到节点 ui 的边。

对于范围 [0, n - 1] 中的每一个节点 i ，你的任务是分别独立计算最少需要多少次 边反转 ，从节点 i 出发经过 一系列有向边 ，可以到达所有的节点。

请你返回一个长度为 n 的整数数组 answer ，其中 answer[i] 表示从节点 i 出发，可以到达所有节点的 最少边反转 次数

提示：

2 <= n <= 1e5
edges.length == n - 1
edges[i].length == 2
0 <= ui == edges[i][0] < n
0 <= vi == edges[i][1] < n
ui != vi
输入保证如果边是双向边，可以得到一棵树。

示例一：

示例 1

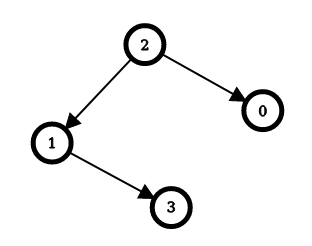
输入：n = 4, edges = [[2,0],[2,1],[1,3]]
输出：[1,1,0,2]
解释：上图表示了与输入对应的简单有向图。
对于节点 0 ：反转 [2,0] ，从节点 0 出发可以到达所有节点。
所以 answer[0] = 1 。
对于节点 1 ：反转 [2,1] ，从节点 1 出发可以到达所有节点。
所以 answer[1] = 1 。
对于节点 2 ：不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[2] = 0 。
对于节点 3 ：反转 [1,3] 和 [2,1] ，从节点 3 出发可以到达所有节点。
所以 answer[3] = 2 。

示例二：

示例 2

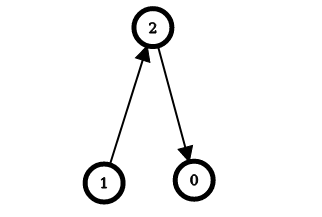
输入：n = 3, edges = [[1,2],[2,0]]
输出：[2,0,1]
解释：上图表示了与输入对应的简单有向图。
对于节点 0 ：反转 [2,0] 和 [1,2] ，从节点 0 出发可以到达所有节点。
所以 answer[0] = 2 。
对于节点 1 ：不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[1] = 0 。
对于节点 2 ：反转 [1,2] ，从节点 2 出发可以到达所有节点。
所以 answer[2] = 1 。

解决方案：

深度优先搜索

我们可以将图看作一个树（将所有的有向边看着无向边，并假设 0 为根节点），对于每个节点：

它到它的子节点要么无须反转（父节点指向子节点），要么需要反转 1 次（子节点指向父节点）
它到它的父节点要么无须反转（子节点指向父节点），要么需要反转 1 次（父节点指向子节点）

利用 1，我们可以进行一个深度优先 dfs1 搜索计算出根节点到达其他所有节点需要反转多少次。

利用 2 以及 dfs2 计算出的反转次数，我们可以计算出每个节点到达其他所有节点需要反转多少次。

代码：

class Solution {
private:
    vector<vector<int>> in;  // 记录每个节点的入边的另一个节点
    vector<vector<int>> out;  // 记录每个节点的出边的另一个节点
    vector<int> rst;  // 记录每个节点到其他所有节点需要反转的次数，即答案
    int dfs1(int root, int fa)
    {
        int cnt = 0;
        for(auto &next : in[root])  // 对每个入边
        {
            if(next == fa)
                continue;
            cnt += dfs1(next, root) + 1;  // 即其子树到达其子树的子树的节点的反转次数加上此节点到达该子树的反转次数（1）
        }
        for(auto &next : out[root])  // 对每个出边
        {
            if(next == fa)
                continue;
            cnt += dfs1(next, root);  // 同上，但是次节点达到该子树不需要反转
        }
        return cnt;
    }

    void dfs2(int root, int cnt, int fa)  // cnt 即 root 到达其他所有点需要反转的次数，我们需要计算 root 的各子节点到达其他所有节点需要反转的次数
    {
        rst[root] = cnt;
        for(auto &next : in[root])  // 对于入边
            if(next != fa)
                dfs2(next, rst[root] - 1, root);  // next 到其他节点的反转次数即 root 到达其他节点的反转次数 - 1，这个 1 即 next 到达 root 不需要反转
        for(auto &next : out[root])  // 对于出边
            if(next != fa)
                dfs2(next, rst[root] + 1, root);  // next 到其他节点的反转次数即 root 到达其他节点的反转次数 + 1，这个 1 即 next 到达 root 需要反转
    }
public:
    vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {
        in = vector<vector<int>>(n);
        out = vector<vector<int>>(n);
        rst = vector<int>(n);
        for(auto &e : edges)
        {
            int x = e[0], y = e[1];
            in[y].emplace_back(x);
            out[x].emplace_back(y);
        }
        dfs2(0, dfs1(0, -1), -1);
        return rst;
    }
};

时间复杂度： $O(n)$ ；空间复杂度： $O(n)$ 。n 为节点的个数。

记录 LeetCode 第 113 场双周赛

战局详情

题目及解答